艺术学理论学科视野下的中国艺术史体例研究

      前不久，笔者有幸参加了宁波市第七届中小学学科骨干教师评比，其中课堂教学评比环节的课题为人教A版《数学（必修2）》第二章的新课“点到直线的距离”.《普通高中数学课程标准（2017年版）》（以下简称《新课标》）对其知识目标描述为：探索并掌握点到直线的距离公式.其知识目标越“简约”，抛给执教者的留白就越多，对其定位难度也越大.

      笔者的思考经历了两个阶段：

      第一阶段：选择哪几种方法推导点到直线的距离公式？“定义法”这个思路是否要贯穿整节课？

      第二阶段：每种推导方法为了凸显什么？本节课的“灵魂”是什么？

      教学目标应该体现数学学科素养，笔者最终抓住“素养”这一把手，如此定位教学目标：用坐标法贯穿始终，通过体验定义法与几何优化在解析几何运算中的策略实施，在解析几何问题中落实数学运算核心素养.

      一、回顾旧知，启发思想

      教学片段1 给出知识框图（如图1），回顾本章已学内容，归纳何为解析几何思想——利用坐标系通过代数法解决几何问题的思想方法即为解析几何思想方法或者坐标法思想.

      

      设计意图 本片段看似简单，实则起到了对本节课核心数学思想的定位作用，能启发学生应用解析几何思想方法解决相关问题.同时，从学过的知识中归纳并感知解析几何思想方法，符合从具体到抽象、从感性到理性的认知规律，符合直观性教学原则，让学生直接感知了教学对象，正如陶行知先生所说的“接知如接枝”.

      二、单刀直入，阐述思想

      教学片段2 教师提出以下两个问题：

      问题1 什么是点P到直线1的距离？

      问题2 如何求点P到直线1的距离？

      对于问题1，初中教材就已给出解释：点P到直线l的垂线段的长度即为点线距离.此外，笔者还从最值角度补充了一个性质：点P到直线l上所有点距离中垂线段最短.

      有了问题1的铺垫，学生顺利地从定义出发得出了求点线距离的方法步骤（如下页图2）.

      

      追问 要得到点P的坐标以及直线l的方程，首先需要做何准备？

      学生思考片刻后明白了一切的基础是“建系”.步骤如下：（1）建立坐标系，用坐标表示有关的量；（2）进行有关代数运算；（3）把代数运算结果“翻译”成几何关系.

      设计意图 本片段的教学目的有两个：概念界定和步骤阐述.数学概念作为对现实对象在数量关系和空间形式上的本质反映，本身亦是一种思维形式.正确理解点到线的距离概念是推导点线距离公式的前提，也就是“源”.“源”决定“流”，因此学生容易想到定义法.此时，顺势给出坐标法解决问题的基本步骤既是思想总结也是方法应用，更是凸显解析几何这一本质，有利于学生抓住纲领，可谓点睛之笔.同时，把一个平面几何问题通过构建数学模型来推导其公式，有效渗透了数学建模的思想.

      三、小组合作，应用思想

      教学片段3 让学生经历定义法中的运算过程.因其运算繁杂，学生个体进行运算势必效率低下，且无法顾及运算能力较差的学生，因此笔者采取以4～5人为一组的小组合作方法，用集体合作运算破解计算难题.这一过程总结如图3所示：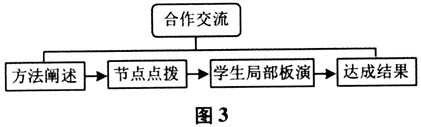

      

      设计意图 本片段是本节课的“定性之为”，凸显了数学运算核心素养这一灵魂.人教A版《数学（必修2）》的教师教学用书中对这一教学过程如此描述：虽然这个过程计算比较繁，但是，教学是一个过程，在这个过程中学生的知识、能力、意志品质都得到了发展.

      “算”的根本目的是为了凸显解析几何的运算属性，提高学生的数学运算素养.因为在实战时往往缺少技巧，所以还得立足于算.另外，教学实效告诉我们，小组合作这一策略也是成功的，能够有效解决因计算进度拖沓而影响教学任务完成这一问题.

      四、类比总结，深掘思想

      教学片段4 利用学生刚才切身体会的计算之繁杂，提出如何进行计算优化.

      任务1 在定义法这一方法主旨下进行计算优化.

      直线l及其垂线方程变形如下：

      

      式（1）、式（2）平方后再相加，可得

      

      优化运算策略1 整体代换（点坐标设而不求）.

      任务2 利用平面几何知识简化代数运算.

      学生自然地想到面积法，步骤如图4所示：