事件、话语及微观史　　

      在最近高二年级开展的一次地市之间“同课异构”研讨活动中，三节以“充分条件、必要条件”为课题的研讨课竟经历了大致相同的教学过程，不禁引发了笔者对目前高中数学课堂教学设计的思考.下面以其中一节典型教学设计案例作反思探讨.

      一、教学设计案例

      1.引入课题

      回顾“命题”的概念；利用例1巩固“判断命题真假”.

      例1 若lna＞lnb，则a＞b；若a＞b，则lna＞lnb.

      2.充分条件、必要条件的定义

      通过例1“若p，则q”的形式，引出充分条件、必要条件的概念：

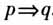      “若p，则q”为真命题，是指由p通过推理可得到q，即由p可推出q，记为.此时p是q的充分条件.

      “若p，则q”为假命题，那么由p推不出q，记为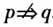.此时p不是q的充分条件.

      判断例1中的充分条件、必要条件的情况.

      3.充分条件与必要条件的判断方法

      定义法：通过定义来判定.

      

      集合法：设集合A=｛x｜p（x）｝，B=｛x｜q（x）｝，若x具有性质p，则x∈A；若x具有性质q，则x∈B.若p是q的充分条件，则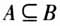；若p是q的必要条件，则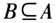；若p是q的充分不必要条件，则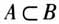；若p是q的必要不充分条件，则.

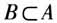      例3 已知p：-2≤x≤10，q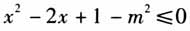：（m＞0），若q是p的充分不必要条件，求实数m的取值范围.

      4.课堂练习与小结部分（略）

      二、对案例的分析与反思

      评课议课是教学研讨的必需环节.在接下来的议课中，很多听课教师就这次活动中的教学常规各抒己见，氛围还算融洽，优缺点也都大多点到，这就是评课议课的重要性！但据笔者观察，还需从以下几个方面去深入反思.

      1.要注重与新教材的对接与融合

      根据《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》（以下简称《意见》），要求从2019年秋季学期起，全国各省（区、市）分步实施新课程、使用新教材并提出了课程实施的工作目标、实施步骤、重点任务和工作机制等，其中2018年启动高考综合改革的省份，可以于2019年或2020年秋季学期高一年级起实施新课程、使用新教材.湖北是2018年启动高考改革省份之一，但在2019年秋季学期的高一年级并没有使用新教材，同样对于正在高二年级的学生面临的是新高考！因此，笔者认为新教材目录和内容是“三新一旧”背景下新课教学必须参照的资料之一！在新教材的目录中，“充分条件与必要条件”已经被编入预备知识第一章“集合与常用逻辑用语”的第四小节.它的课程定位是为高中数学学习做好学习心理、学习方式和知识技能等方面的准备，帮助学生完成初高中学习的过渡，因为“逻辑”是数学语言的重要部分，是“学会用数学语言描述世界”的必备条件.2019年5月，在成都人民教育出版社A版新教材培训会议上，新教材编者王嵘老师在提到第一章“集合与常用逻辑用语”的编写思路时说道，“常用逻辑用语，在回顾命题的基础上，选取初中典型的数学命题，学习新知识特别是充分条件、必要条件、充要条件和判定定理、性质定理、数学定义之间的关系”.因此，新教材在紧密联系初中学习过的典型数学命题，通过分析、判断、归纳等方法逐步形式化或符号化提升学生的逻辑推理素养.例如，新教材第一个思考和例1中通过给出“平行四边形是菱形”“a//b”“四边形是平行四边形”“两个三角形相似”的一个充分条件，其目的是引导学生将充分条件与判定定理联系起来.新教材中第二个思考让学生给出“四边形是平行四边形”的其他充分条件，其目的是让学生认识到平行四边形的每个判定定理实际上都给出了“四边形为平行四边形”的一个充分条件.从这个角度看，前面的教学内容明显缺乏这方面的教学设计，而更多的是例题的讲解和习题的处理.