中国高考评价体系(以下简称“高考评价体系”)的出台,奠定了我国新时代高考改革的理论基础与方法论基础.高考评价体系提出“一核四层四翼”的整体评价框架,其中“四翼”是对高考考查要求的凝练,包括基础性、综合性、应用性、创新性,回应了高考“怎么考”这一关键问题.关于“四翼”要求,“基础性”强调基础扎实,“综合性”强调融会贯通,“应用性”强调学以致用,“创新性”强调创新意识和创新思维.[1]其中,基础性与综合性是我国高考长期以来的考查重点,而应用性与创新性则是近年来的关注要点,反映出国家对应用型人才与创新型人才的重视和需求. 问题情境是高考评价的考查载体,基于知识应用和产生的方式的差异,问题情境被划分为两类:生活实践情境、学习探索情境.[2]由问题情境产生的复杂情境活动,与高考的“应用性”和“创新性”考查要求相对应. 2020年高考是“四翼”要求明确提出后的首次高考,其试题命制具有极强的典型性与引领性.本研究对2020年高考数学试题中落实“应用性”与“创新性”的问题情境进行分析,借此了解相关理念如何落地,并提出相应的教学建议,助力“高考引导教学”这一目标的达成. 一、落实“应用性”要求的两种类型 落实高考评价体系中的“应用性”要求,关键在于通过各式各类的生活实践情境,考查学生应用数学的能力与素养,让学生深刻感受数学的应用价值.依据数学应用在问题情境中的作用,可将其分为两类:解困应用、说理应用. (一)解困应用:以数学工具解决现实问题 数学的工具性价值,使其成为解决现实问题的重要手段.为发挥高考的正向引导作用,高考试题要坚持理论联系实际,选取来自现实生活中的真问题,使学生在问题解决中掌握知识、培养能力、提升素养,真切感受到数学在现实生活中的价值. 例1[2020年高考理科数学全国Ⅱ卷第3题] 在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05.志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者( ) A.10名 B.18名 C.24名 D.32名 例1以紧密结合当前社会形势的新冠肺炎疫情为大背景.由于网络销售能够减少人与人之间的接触,自然成为疫情防控期间的重要销售模式,但订单量大幅增加却引发了订单积压的问题,这便构造出一个现实困境,根据积压订单数、预计的次日新增订单数、志愿者的人均日配货数等信息对所需志愿者人数进行合理估计,便成为一项非常有价值的数学任务.在这样一个拟真实的情境中,学生需要考虑各要素之间的数学关联性,还需准确理解“超过1600份的概率为0.05”“积压订单及当日订单的配货的概率不小于0.95”的含义及其对问题解决的影响,让学生考虑生活中的事件发生的概率大小,使问题情境更加真实. (二)说理应用:以数学语言阐明事物机理 在现实生活中,许多事物发生、运行的机理很难一眼看清,如何将具象转化为抽象,帮助人们更好地认识事物背后的机理呢?这时候就可以考虑借助数学的手段,以数学的语言阐明问题情境的发生缘由、形成机理. 例2[2020年高考文科数学全国Ⅱ卷第3题]
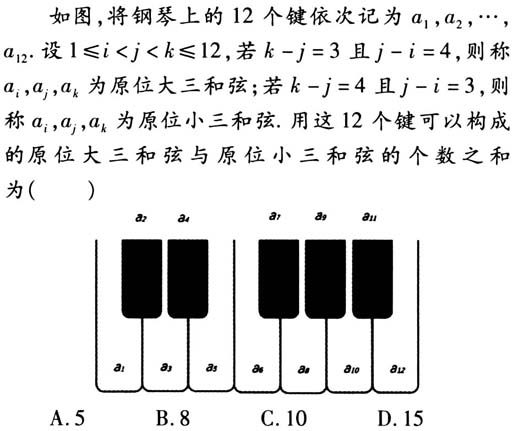
例2以钢琴和弦为背景,考查学生对于和弦概念的数学表达形式的理解.这一钢琴和弦情境是数学与音乐的有机结合,要求学生能够借助数学认识原位大三和弦、原位小三和弦的数学表达形式.处理这一问题情境自然离不开数学的应用,这里的“应用”并非指应用数学解决现实问题,而是应用数学说明乐理,考查学生是否具有“用数学的眼光看世界”“用数学的语言表达世界”[3]的能力. 二、落实“创新性”要求的两个方面 落实高考评价体系中的“创新性”要求,目的在于培养学生的创新思维与能力.“创新性”要求的落实,关键在于设置非常态化的问题情境,为学生营造出创新思维的培养皿.基于问题情境中所体现创新的不同方面,又可将其具体划分为:背景创新、设问创新. (一)背景创新:以陌生情境打造问题空间 问题情境的背景创新,是指问题情境的背景体现出的创新性,这被视为高考题情境创新的重要体现形式.[4]设置日常生活中学生熟识的问题情境,可能会降低情境对学生在认知方面带来的挑战,容易使其陷入程序化的解题进程之中.这时候,陌生的问题情境背景就显示出其独特价值,有助于学生展开非常规化的思考. 例3[2020年高考理科数学全国Ⅲ卷第4题] Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数Ⅰ(t)(t的单位:天)的Logistic模型:
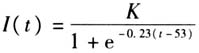
,其中K为最大确诊病例数.当I(
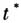
)=0.95K时,标志着已初步遏制疫情,则
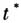
约为(ln19≈3)
 例2以钢琴和弦为背景,考查学生对于和弦概念的数学表达形式的理解.这一钢琴和弦情境是数学与音乐的有机结合,要求学生能够借助数学认识原位大三和弦、原位小三和弦的数学表达形式.处理这一问题情境自然离不开数学的应用,这里的“应用”并非指应用数学解决现实问题,而是应用数学说明乐理,考查学生是否具有“用数学的眼光看世界”“用数学的语言表达世界”[3]的能力. 二、落实“创新性”要求的两个方面 落实高考评价体系中的“创新性”要求,目的在于培养学生的创新思维与能力.“创新性”要求的落实,关键在于设置非常态化的问题情境,为学生营造出创新思维的培养皿.基于问题情境中所体现创新的不同方面,又可将其具体划分为:背景创新、设问创新. (一)背景创新:以陌生情境打造问题空间 问题情境的背景创新,是指问题情境的背景体现出的创新性,这被视为高考题情境创新的重要体现形式.[4]设置日常生活中学生熟识的问题情境,可能会降低情境对学生在认知方面带来的挑战,容易使其陷入程序化的解题进程之中.这时候,陌生的问题情境背景就显示出其独特价值,有助于学生展开非常规化的思考. 例3[2020年高考理科数学全国Ⅲ卷第4题] Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数Ⅰ(t)(t的单位:天)的Logistic模型:
例2以钢琴和弦为背景,考查学生对于和弦概念的数学表达形式的理解.这一钢琴和弦情境是数学与音乐的有机结合,要求学生能够借助数学认识原位大三和弦、原位小三和弦的数学表达形式.处理这一问题情境自然离不开数学的应用,这里的“应用”并非指应用数学解决现实问题,而是应用数学说明乐理,考查学生是否具有“用数学的眼光看世界”“用数学的语言表达世界”[3]的能力. 二、落实“创新性”要求的两个方面 落实高考评价体系中的“创新性”要求,目的在于培养学生的创新思维与能力.“创新性”要求的落实,关键在于设置非常态化的问题情境,为学生营造出创新思维的培养皿.基于问题情境中所体现创新的不同方面,又可将其具体划分为:背景创新、设问创新. (一)背景创新:以陌生情境打造问题空间 问题情境的背景创新,是指问题情境的背景体现出的创新性,这被视为高考题情境创新的重要体现形式.[4]设置日常生活中学生熟识的问题情境,可能会降低情境对学生在认知方面带来的挑战,容易使其陷入程序化的解题进程之中.这时候,陌生的问题情境背景就显示出其独特价值,有助于学生展开非常规化的思考. 例3[2020年高考理科数学全国Ⅲ卷第4题] Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数Ⅰ(t)(t的单位:天)的Logistic模型: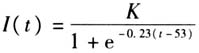 ,其中K为最大确诊病例数.当I(
,其中K为最大确诊病例数.当I(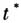 )=0.95K时,标志着已初步遏制疫情,则
)=0.95K时,标志着已初步遏制疫情,则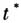 约为(ln19≈3)
约为(ln19≈3)