一个国家、一个民族不能没有灵魂

      随着新课程改革的不断深化，跨学科教学已经成为实现新课改目标的重要途径.跨学科是指打破学科的界限，将不同学科融合在一起的教育和科研活动，其优势主要在于在多门学科之间交叉，利用不同学科的知识来研究同一个问题，打破单一学科的局限性.《普通高中数学课程标准（2017年版）》（以下简称《课标（2017年版）》）的基本理念中也强调数学与生活以及其他学科的联系，提升学生应用数学解决实际问题的能力[1].基于此，笔者以跨学科的视角对新人教A版高中数学必修教材进行分析，探讨我国目前高中数学必修教材中跨学科的总体情况.

      一、研究对象与分析框架

      （一）研究对象

      人民教育出版社依据《课标（2017年版）》编写的2019年新人教A版高中数学教材正式发布，已于2019年秋季在全国范围内正式使用[2].新编写的教材，必修五本教材缩减为两本，将必修第一册和必修第二册定义为基础练习，让学生在必修阶段完成高中数学的基础知识练习.基于此，本文对新人教A版高中数学必修教材部分两册共计十个单元从“跨学科”角度进行分析，为高中数学教学提供参考.

      （二）分析框架

      以“教材跨学科”为主题词在中国知网进行检索，一共有26条结果，其中关于数学教材跨学科研究的文献甚少.有学者直接进行跨学科研究[3]，通过比较中美初中数学数与代数部分得出数学教材与物理学、经济学的联系紧密.有学者研究数学文化时将跨学科内容作为一部分，如张维忠教授等指出国内外注重在数学课程改革中通过数学与其他学科整合的形式展现数学文化多元性的理念[4].还有研究者指出数学教学要实现多学科的融合，促进学生全面发展.基于已有研究，从跨学科视角出发综合其他学者建立本研究的分析框架[5]，对我国新人教A版高中数学必修教材部分进行统计分析.该框架由学科来源、分布位置、使用目的和呈现方式四部分组成.其中，学科来源是以《中华人民共和国学科分类与代码国家标准》（2009年版）（简称《学科分类与代码》GB/T137452009）为标准，将学科分为自然科学、人文与社会科学类、医药科学类、工程与技术科学类、农业科学类.分布位置有五个子分类，使用目的和呈现方式各3个子维度，具体如下页表1.

      

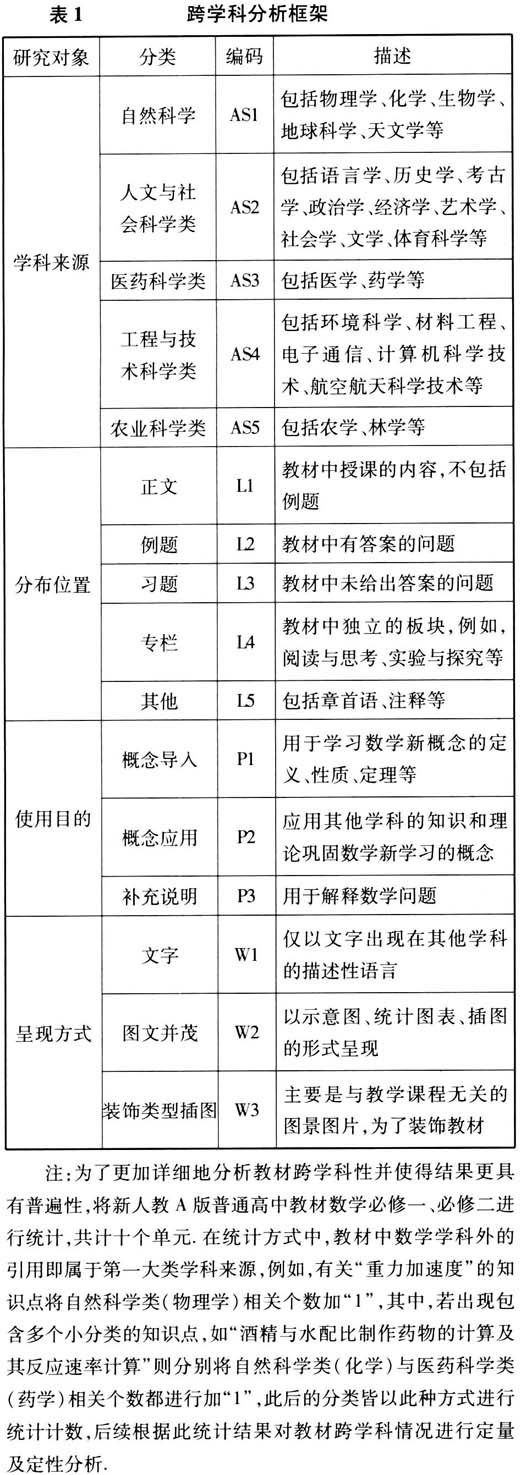      二、跨学科内容分析

      （一）跨学科内容的学科来源分析

      从跨学科内容的学科来源可以看出（下页图1），新人教A版高中数学必修教材中均涉及自然科学、人文与社会科学、农业科学、工程与科技科学、医药科学五个门类.其中自然科学的相关个数为197个，占总数的41%，在人教A版占据了较大比例，这也显示出了现代数学教材与学生生活密切的联系，较好地体现跨学科性.从所统计教材的教育对象来看，大部分受教育对象都是高中生，对除自然科学外的门类接触较少，因此在教材中加入其他跨学科的知识点能有效地弥补其他门类的不足.

      

      对比所统计教材的必修一与必修二，发现必修二将自然科学还是作为主要着重点，增加了农业科学知识点，但人文与社会科学知识点大大减少.从总体上看，必修一和必修二涉及的跨学科数目基本一致，但是必修一着重自然科学与人文社会科学门类，必修二着重自然科学与农业科学门类.由此可见，高中教材虽然有所涉及跨学科，但在不同时期也仅仅着重一两个门类进行教学，这样跨学科教学的因时制宜会更具有针对性.《课标（2017年版）》中也提出：“强调数学与生活以及其他学科的联系，提升学生应用实际解决数学问题的能力，加强数学文化的渗透”[1].优化课程结构是现在数学教材所着重进行的变革，为学生发展提供共同基础及多样化选择.数学不仅是一门科学，而且也是一个多元化的系统，包含了大量的经济学、生物学、自然科学、体育与健康等学科的知识点.目前新人教A版高中数学教材将其他学科加入其中，也能引导学生更好地理解所学知识.

      （二）跨学科内容的分布位置分析

      从分布位置上看（见下页图2），有以下结论：（1）新版高中数学必修教材跨学科内容以习题为主.习题是课堂教学内容的巩固和深化，在培养学生核心素养方面发挥着重要的作用，所以教材在习题的编选方面更重视整体性.（2）专栏跨学科的数量仅次于习题.在统计过程中发现每个章节都会有一个专栏，大部分专栏通过介绍与章节有关的历史人物来描述概念的发展过程，加深学生对新概念的学习.（3）正文和例题跨学科内容较均匀，其他（解释性文字）涉及跨学科的内容较少.章首语和注释是对所学知识的导入和延伸，在教材编写的过程中也要重视这部分的编排.（4）在统计过程中发现，复数章节跨学科内容主要集中在专栏，对有关历史人物的介绍，正文、例题、习题几乎未涉及跨学科，其原因是复数是实数集的扩充，很难在情境中和其他学科体现出来.