课程理论和实践发展至今，教育家为解决课程内部的逻辑统一问题，提出了直线型课程和螺旋型课程两种不同主张。它们均具有合理的一面，同时又具有自身不可克服的缺陷。那么，是否存在另一种能更深刻地实现课程内部的逻辑统一的新型课程？如果存在，这种新型课程的科学依据和客观规定性是什么？它的基本特性是什么？探明这些问题，无疑对课程理论和实践都具有重要意义。 一 直线型课程和螺旋型课程的缺陷 国内学者一般只提直线式教材排列，它是指：“一科教材内容采取环环紧扣、直线推进、不与重复的排列方式。”[1]不过，这种观点上升到课程的层次来看，就是直线型课程的主张。 重工具价值、重知识传递功能、重人文道德教育和采用死记硬背的方法，是直线型课程的显著特点。它在实践中面临的问题主要有：1.由于经济发展的制约作用，许多儿童只能接受初等教育。在这种情况下，如果在初等教育阶段采用分科的直线型课程，就必须设置大量科目，这样就必然使教育内容庞杂，量过多，加重学生负担；如果采用综合的直线型课程，一门课程包含若干学科的内容，直线型结构就无法实现了。2.知识经验的分门别类至今尚是一个悬而未决的难题，即使按现在人们比较一致的公认分类方法，仍然存在知识逻辑与学生心理逻辑的矛盾。在直线型课程的定型时期，人们是基本不考虑儿童心理发展规律的。因此，在特别强调适应和促进学生发展的当代教育中，直线型课程的已有范型，具有先天不足后天无法弥补的致命缺陷。3.当代科技的飞速发展使各个领域的知识经验相互交叉，无论怎样从中精选一部分出来作为课程内容，它们相互交叉的性质不会变。因此，课程无论怎样分科，相互间总会相互联系而相互交叉；课程内容无论怎样精细地分环节安排，各个环节之间总会在不同层次上出现重复。所以，严格意义上的直线型课程已成为历史，在现代教育实践中是无法实现的。 本世纪50年代末，布鲁纳提出了螺旋型课程的概念，但未作深入研究。后来，拉盖恩和谢菲尔德又对其进行了探讨，指出：“螺旋型课程是一种教材排列方式，这种排列方式使教材在学程的每一时刻反复出现，让学生在科目上逐步深入或学习科目的一个方面。”[2]进而，福谢简单明了地解释道：“螺旋型课程是设计来让学生随着不断的成熟，在其学习过程中逐步深入。一门科目在一个年度中的内容可以延伸到许多年度。”[3] 螺旋型课程的主张，曾经促进了课程设计和教材编写的观念和技术的发展。然而，理智地对现有的螺旋型课程的观念进行一番分析，就令人疑雾重重了。第一，在一门课程或科目中，怎样才能实现其螺旋型结构？如果象布鲁纳所言：“人们肯定能够使六岁儿童了解极限的概念，其正确途径就是让儿童领会微积分中的基本概念。”[4]那么，知识自身客观上具有的层级结构就被否认了。极限本身就是微积分的基本概念，再用微积分的基本概念去解释极限而让六岁儿童了解极限的概念，这可以说是在玩无聊的文字游戏了。第二，知识客观上可以从不同角度分类，而不同类型的知识又往往是联系在一起的。这样，对具体知识内容的排列来说，从这一种分类角度看是螺旋型排列，而从另一个分类角度看却又是直线型排列。比如小学数学课程中的四则运算，将其按“整数四则运算→小数四则运算→分数四则运算”排列。从四则运算的分类来看，这似乎是螺旋型排列了；但从数的分类来看，则似乎又是直线型排列了。诸如此类的问题，与其说是螺旋课程理论尚待研究的课题，不如说是螺旋型课程自身局限所难以克服的难题。 深入分析直线型课程和螺旋型课程存在的缺陷和问题的根源，我认为，主要在于这两种主张都未揭示课程内容作为一种再生性文化所具有的特殊性质。中小学课程内容，从形式上看，可以概括地划分为为数不多的不同科目，不同科目自身又可划分出若干知识系列；从内容上看，不同的知识在知识层级结构中具有自身的独特位置；从内容的内核看，又凝结着人类的不同能力及其不同的水平。这样，复杂的形式、复杂的内容和复杂的内核之间，便构成了极其复杂的关系。这些复杂的关系，无论直线型课程还是螺旋型课程均无法完全驾驭。 二 事物发展的逻辑型规律 课程结构客观上是被个体发展、社会发展、文化发展以及教学活动等分别地制约着和综合地决定着，实现课程内部的逻辑统一，实质上就是在课程结构中实现儿童发展逻辑、社会发展逻辑、文化发展逻辑和教学活动逻辑之间的有机统一。显然，使这些逻辑得以统一的新型课程，必须以事物发展的某一普遍性规律为客观依据和基础。经过分析和比较，我们发现对寻找能实现课程内部逻辑统一的新型课程最具启发意义的普遍性规律是“逻辑型”规律。 （一）逻辑型规律的基本内涵 人类在经过长期观察和实践之后，通过科学的分析、比较和综合，发现许许多多自然现象和社会现象在发展变化过程中，都具有一种“逻辑型”规律。科学学把这一规律形象化为平面坐标里的一条曲线（见图1），它是由一条指数曲线和一条对数曲线连接而成，呈"S"型，故这一规律又称为"S"规律。它的基本内涵可以从两方面加以概括：
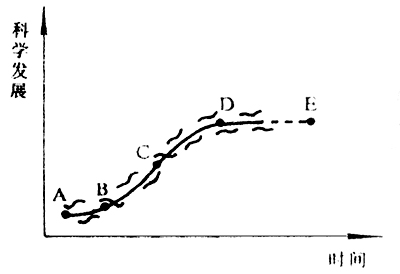
图1 事物发展的逻辑型规律曲线 一方面，事物发展明显区别为连续的四个阶段。图1表明，事物发展在一定时区里，随着时间的推移，一般总要经历四个不同增长趋势的阶段。第一阶段（即曲线的AB段），在相对较长的时间内缓慢而持续地增长。第二阶段（即曲线的BC段），在较短时间内急剧地加速增长。第三阶段（即曲线的CD段），在较短时间内减速增长。第四阶段（即曲线的DE段），在较长时间内处于稳定平衡状态。四个阶段构成了事物在一定时期内的动态变化进程。 另一方面，一系列"S"型小过程构成一个整体的"S"型大过程。在无限的时空里，事物的发展变化是无限的。每一事物在一个"S"型发展变化过程的第四阶段的平衡状态里，都产生着旧质的衰微和孕育着新质的发展，于是另一个"S"型发展变化的过程便在更高水平上展开，……一系列"S"发展的小过程便构成了一个整体的"S"型发展的大过程。
