教育与负面性：

      以日常用语我们可以将负面经验描述为那些我们不愿遭遇的经验， 如与周边环境和人交往中遭遇到的失望，由于意料之外的疾病带来的烦躁，或者由于自然灾害引起的震惊等。失望、烦躁与震惊所描述的消极经验告诉我们，他人、自我或者自然界突然表现得出乎我们的意料，出乎我们的习惯。这类负面经验有时会让我们感觉到，与朋友、与环境的关系受到了干扰。但在教育过程中，这些经验并不是那么消极，反之通过这些负面性还能获得积极的意义。

      在此我们论述负面经验在教育、教育学以及教师教育中不可忽略的作用。 我们认为人类经验表现出它特有的负面性，没有这类负面性所有人类思维和活动领域中的学习不可能进行。我从四个方面进行探讨：1 ）经验负面性在人类教与学过程中的决定性作用；2）经验负面性对教育过程的意义；3）负面经验对批判性研究教育科学的重要性；4）负面经验对教师教育的可能意义。

      一、教育、教养与经验负面性

      教与学过程和经验负面性之间有着密切联系，这并不是一个全新的观点， 我们可以追溯到古代哲学上来探讨这个观点。在欧洲传统中， 从柏拉图关于“枚农（Menon）”对话可见早期对学习、经验以及教学之间关系的讨论。在这个“枚农”对话中，苏格拉底试图诱导一个还不懂数学几何事实的小男孩，去认识正方形与直角三角形之间的几何关系。

      柏拉图的这个对话指出了人类教与学过程中负面经验的意义， 它们体现在以下三个方面：

      ——对话中存在着一个矛盾观点，即在小男孩不知道并不会做的事情中， 已经包含了他通过学习将获得的“正确想法”。[1]（p.85c）

      ——著名的受到改革教育学派重视的陈述：看这个小男孩“不用教他”就在学了。[1]（p.85d）

      ——对话最后的讨论反映了整个谈话过程的实用主义观点， 即某人即使从来没有走过某个城市的路，也能引导他人到那里去，只要他有对这条路的“正确观念”。[1]（p.97a—b）

      这三个观点刻画出关于人类教与学结构的基本看法， 我们用小男孩在与苏格拉底对话中学习数学的例子加以说明。

      根据第一个观点，学习总是从已经获得的观念出发， 这些观念揭示出与学习者尚未知道的观念的联系。学习并不是毫无条件的知识和能力的获得过程，而是这样一种过程，即在这过程中有关学习者自身知识以及无知的经验、有关能力以及无能的经验起着重要作用。那个小男孩学会认识几何关系，并不是因为他自发地或根据教师的要求给出正确答案，而是受苏格拉底提问的支持，使他进入学习过程中，在这个学习过程中他对相关事实展开想象，部分地认识到问题并认识到自己的无知。

      这个小男孩通过失望和混淆，即通过负面经验，找到了苏格拉底所提问题的答案，即哪个正方形是这个2×2正方形或者称“4块型”正方形的两倍大（图1）。

      

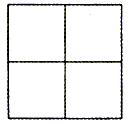      图1： 2×2正方形

      他首先给出的答案是那个4×4或者称为“16块型”的正方形（图2）。

      

      图2： 4×4正方形

      然后他发现自己回答的正方形，只是其周长为2×2正方形周长的两倍，面积却是2×2正方形面积的四倍。

      这个错误答案在后面问题的解答中起关键作用， 没有经历这个错误他可能就找不到答案。在小男孩发现这个4×4正方形是错误答案后，他先尝试在这个大正方形中寻找答案。他找出了3×3正方形或者称“9块型”正方形这个答案。 紧接着他又发现，这个正方形比“4块型”正方形的两倍多了一块1×1正方形（图3）。

      

      图3： 4×4正方形中的3×3正方形（阴影部分）

      这个3×3正方形也不是苏格拉底问题的正确答案，这使得小男孩束手无策。 他承认，经历了这些误解和负面经验后，不知道哪里去寻找这个正方形。在此他仅仅尝试了所有水平直线构成的正方形，在这个图形中似乎不可能有这类“8 块型”的正方形。

      这时苏格拉底给了这个束手无策、但还一直在寻找答案的小男孩关键的提示。 他“指了指”2×2正方形上的那条对角线。（图4）

      

      图4： 2×2正方形上的对角线

      借助苏格拉底指点的对角线，小男孩在他前面给出的错误答案即4×4 正方形中发现了要找的答案。他观察着并且认识到这个由四条对角线构成的“8 块型”正方形，而这之前他不能在4×4正方形上找到“8块型”正方形的位置。

      他通过比较被对角线划分的4个“4块型”正方形的面积， 推断出由这四条对角线组成的正方形就是要寻找的“8块型”正方形。（图5）