中图分类号：O221.4 文献标识码：A 文章编号：1007－9807 （2002）01－0035－05 修订日期：2001－11－26。 0 引言 信息技术和通讯技术的飞速发展，推动了市场的全球化进程。客户化需求和单件化生产使得企业面临严峻的考验，如何有效地管理企业运作是今天全球竞争环境下的一个极具挑战性的领域。虚拟企业作为一种新的制造模式，通过联合具有不同核心能力的合作企业，迅速集成各成员公司在业务、知识、信息、制造资源等方面的优势，占领市场共同面对市场竞争。从而提高企业的生存能力，实现双赢。企业为了参与联盟必须提高企业的敏捷能力，利用企业的信誉和能力通过竞争为核心公司吸收［1，2］。如何有效地制定竞标策略直接关系企业能否通过竞争进入虚拟企业，获得市场机遇。竞标策略研究成为企业和研究界关注的一个热门课题。 国内外许多文献对竞标决策问题进行了研究，一部分学者依据概率统计理论进行了竞标决策的研究，其中文［3 ］在考虑企业期望利润条件下，给出了一种优化竞标价格的单变量统计模型，文［4 ］提出了企业在不同竞标价格时的获胜概率计算模型。另外，文［5 ］中建立了竞标决策的对策论模型，通过寻找纳什均衡解，从而给出企业的优化竞标策略。但是由于以上模型给出了太多的假设条件，理论性太强，造成模型的可操作性差。并且对于实际竞标过程中存在的大量非定量因素（如企业敏捷度、项目的风险性等）难以有效加以体现。本文将博弈论和模糊综合评价思想相结合，利用两种理论的长处，探讨了一种新的竞标决策方法，给企业进行竞标决策提供了一种新的思路。在文中，首先针对企业参与虚拟企业的原因和联盟对于企业敏捷度的基本要求进行了简要论述。并利用静态博弈得出了竞标价格的可行域，其次利用模糊综合评估法得出企业的获利因子，最后给出了满足企业满意度要求的竞标工期，从而在保证盈利的条件下提高企业中标的可能性。 1 敏捷性与虚拟企业 动态联盟是知识经济浪潮中涌现出来的一种新的管理组织模式，企业通过联盟的根本目的是追求各自利益的最大化，这里利益不但包含短期利益，也包含了长期利益， 同时包含了现金收益和竞争力的增长［6］。而合作双方很可能是处于同一市场或关联市场的竞争者或潜在竞争者。由于虚拟企业必须具有迅速响应市场的能力，客观上要求参与联盟的企业具有敏捷性。即企业的RRS（reconfigurable、reuseable、scalable）［7，8］能力。对于当代企业来说应当提高企业的信誉、信守诺言和协议，并且进行TQM管理。 在制定决策过程中必须对企业进行定位，依据企业在联盟中的地位和本身的能力，并结合预计收益和风险度大小制定合适的竞标决策。 2 虚拟企业协作中的优化竞标策略 动态联盟中企业间存在合作和竞争，各自的综合利益在合作初期难以准确判断，彼此对于联盟的贡献亦难以度量，因此无法以明确的合约加以限定。在竞标策略制定过程中，竞标工期和竞标价格是必须考虑的两个核心问题。首先利用对策论思想［9 ］建立静态博弈模型得到企业竞标价格的可行域，然后通过模糊综合评估法得到企业在联盟中的获利因子。从而给出建议的优化竞标价格。在文中基于竞标满意度和企业成本最小化原则，得出了竞标工期的估计值。 2.1 静态博弈的竞标价格可行域 假设企业A为联盟的盟主，企业B为参与竞争的联盟候选者。联盟的双方通过合作将带来正和的总收益。不妨进一步假设合作中在投入和总收益的分配中，按一定的比例进行。企业的收益函数除了与约定分配比例有关外，还与双方的约定收益之差相关，于是假设I[,0]是合作中的总投入，P[,0]是静态博弈中企业A、B合作的总收入，λ[,1]、λ[,2]为企业投入和分配在总投入和总收入的比例，且λ[,1]≥λ[,2]，λ[,1]＋λ[,2]＝1。同时依据企业间的竞争和合作关系给出企业间的相关系数ψ，且ψ≥0。于是可以得到联盟企业的得益矩阵如下： 表1 联盟企业的得益矩阵
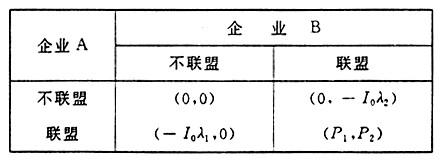
其中P[,1]，P[,2]分别是企业A和B在合作中的纯收益，分别如下式所示： P[,1]＝P[,0]λ[,1]＋（λ[,1]－λ[,2]）P[,0]ψ－I[,0]λ[,1]（1） P[,2]＝P[,0]λ[,2]＋（λ[,2]－λ[,1]）P[,0]ψ－I[,0]λ[,2] （2） 在此博弈中，存在两个纯策略纳什均衡，但必须保证双方的纯收益为正，联盟双方才会采取联盟策略，所以企业B的竞标价格必须满足P[,1]≥0和P[,2]≥0，才有可能参与联盟。于是可以得到投入和分配比例必须满足下列不等式： λ[,1]≥λ[,min]，λ[,2]≥λ[,min] 其中 λ[,min]＝P[,0]ψ／（P[,0]－I[,0]＋2P[,0]ψ） （3） 从式（3）可以看出企业B为了参与联盟，提出的合理竞标价格区间为［P[,0]λ[,min]，P[,0]（1－λ[,min]］， 企业的相关系数ψ越大，意味着企业间的竞争程度越大。同时当ψ一定时，收益率β＝（P[,0]－I[,0]）／I[,0]越大，则企业B的合理竞标价格区间越大。
