艺术与技术

      “函数单调性”是学生在高中阶段学习的第一个函数基本性质，其研究方法对后续函数性质的学习具有示范引领作用；是学生第一次经历用数学符号语言表达数学概念，从而体会数学的简洁美；并且单调性概念的形成过程体现了数学概念逐步抽象的过程，是培养学生数学抽象素养的绝佳素材.因此，有必要对不同教材中的“函数单调性”内容加以比较，并对教师教学提出相应建议.

      一、研究对象

      研究对象为依据《普通高中数学课程标准（实验）》（以下简称03版课标）编写的2007年第2版《普通高中课程标准实验教科书·数学1·必修（A版）》（以下简称2007版教材）[2]与依据《普通高中数学课程标准（2017年版）》（以下简称17版课标）编写的2019年第1版《普通高中教科书·数学·必修第一册（A版）》（以下简称2019版教材）[2]中的“函数单调性”内容.本内容在两版教材中的所处位置见表1.

      

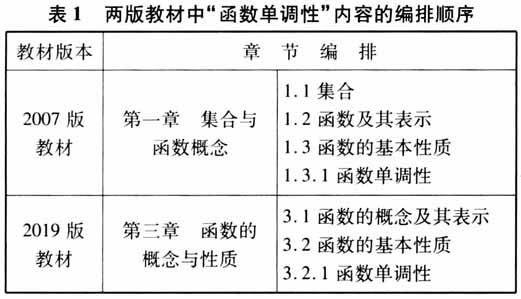
      2007版教材的编排顺序为：1.1集合→1.2函数及其表示→1.3函数的基本性质（第1课时：函数单调性）.2019版教材的编排顺序为：第一章集合与常用逻辑用语→第二章一元二次函数、方程和不等式→第三章3.1函数的概念及其表示→3.2函数的基本性质（第1课时：函数单调性）.

      二、研究结果

      （一）课标要求

      2003版课标对“函数单调性”的要求是“通过已学过的函数特别是二次函数，理解函数的单调性；学会运用函数图象理解和研究函数的单调性.”[3]2017版课标对“函数单调性”的要求是“借助函数图象，会用符号语言表达函数的单调性，理解其作用和实际意义.”[4]

      （二）概念引入

      2007版教材“函数单调性”概念引入遵循“三部曲”：图形语言→自然语言→符号语言，即先从学生熟知的一次函数f（x）=x和二次函数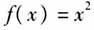的图象入手，观察获得图象“上升”“下降”的直观感知，再取值填表得到“函数值随着自变量的增大而增大或减小”的自然语言描述，最后用数学符号语言刻画这种规律.

      2019版教材“函数单调性”概念引入也遵循“三部曲”：首先，开门见山“在初中，我们利用函数图象研究过函数值随自变量的增大而增大（或减小）的性质，这一性质叫做函数的单调性”；接着以二次函数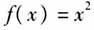为例，先从图象可看到：图象在y轴左侧从左到右下降，即当x＜0时，y随x的增大而减小，接着用符号语言描述，再用同样的方法研究y轴右侧.

      （三）概念表述

      

      （四）概念理解

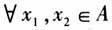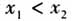      2007版教材在“函数单调性”概念之后，没有对概念进一步加以说明.2019版教材在“函数单调性”定义下设置了“思考”栏目：（1）设A是区间D上某些自变量的值组成的集合，而且，当时，都有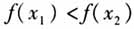，我们能说函数f（x）在区间D上单调递增吗？你能举例说明吗？（2）函数的单调性是对定义域内的某个区间而言的，你能举出在整个定义域内是单调递增函数的例子吗？你能举出在定义域内的某些区间上单调递增但在另一些区间上单调递减的函数例子吗？在这里设置思考，是针对概念中的难点加以说明.思考（1）是针对“函数单调性”概念中的“任意”二字设置的；思考（2）是针对定义中的“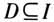”设置的.

      （五）概念运用

      对“函数单调性”概念的运用通过例题、习题设置来分析，这里题数以大题记.

      2007版教材设置2道例题.例1根据给定区间的函数图象，说出函数的单调区间以及在每个单调区间上函数是增函数还是减函数？此例通过图象直观感知函数的单调性，在写单调区间时应注意提醒学生区间端点处的开闭以及多个单调区间的连接问题.例2试用函数的单调性证明物理学中的波意耳定律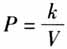（k为正常数）为（0，+∞）上的减函数.此例侧重于“函数单调性”数学形式化定义的运用，解答过程严格按照单调性证明5步骤进行：取值→作差→变形→定号→下结论.例题后设置探究：画出反比例函数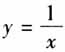的图象，（1）函数的定义域是什么？（2）在定义域上的单调性怎样？并证明.例题渗透数形结合思想，也注重“函数单调性”数学形式化定义的运用.