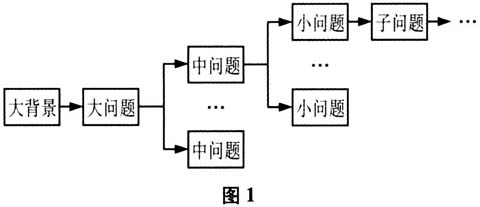
2014年,教育部出台的《关于全面深化课程改革,落实立德树人根本任务的意见》首次提出了“核心素养体系”这个概念,并且将核心素养定义为“适应终身发展和社会发展需要的必备品格和关键能力”.2016年,课题组发布《中国学生发展核心素养》,2017版普通高中各学科的课程标准又相继提出了学科核心素养的框架,提升学生核心素养成为教学改革新的目标要求,在教育部组织的几次关于教材编写的培训会上,相关专家提出了基于核心素养的教材编写的基本要求,其中非常重要的一条是“大背景”,即用真实的背景性材料,让学生经历完整的提出问题、解决问题的过程,在研究问题的过程中建构学科知识体系,他们认为,只有这样,才能真正地发展学生的核心素养.下面是关于苏教版普通高中课程标准教科书(数学)在这方面的探索和思考,一家之言,意在抛砖引玉. 一、“大背景”释义 每一章的“大背景”是蕴含了本章核心思想、数学本质或思维起点的,具有较强生成性的现实材料、数学材料(如“复数”一章)或其他学科的科学材料(如“平面向量”一章),通过对这些材料的研究,可以揭示或提炼出本章的主问题或核心问题(大问题).这个或这些主问题对本章内容起统领作用:或是本章研究的逻辑起点,由主问题进行学科的逻辑发展,就生成了全章的知识结构;或是本章研究的本质问题,通过对主问题的不同层面的研究(并列型)或从简单到复杂,依据数学研究的一般逻辑顺序和方法(递进型)建构本章知识体系,简单地说,所谓“大背景”,就是一章内容的“根”和“源”,章内容的展开就是“大背景”的问题解决的过程. 一章中各节均有节首语,节首语是根据章首语和章首语中提出的本章主问题,以及本章已经研究过的内容,自然地生成的背景材料,并由此背景材料自然地提出本节所要研究的主问题(中问题).节的主问题是服务于章的主问题的,因此也就蕴含于“大背景”之中,其研究内容是围绕“大背景”的某个方面(侧面)而进行的.各小节的中问题就组成了本章问题解决的问题链. 无论是章问题还是节问题,都确保既体现本原性原则:在逻辑起点处提出本章节最本质的问题,揭示本章节内容的核心观念、核心思想;又遵循适宜性原则:起点低、入口浅,但寓意深,让学生能理解、能操作、能探究, 有时一节的主问题就是一节课的初始问题,有时在一节的问题解决过程中又会形成一些新的小问题,也就是解决节的主题的问题链,从而形成了每一堂课的主问题,这些问题链有的是显性的,教材中就展现了,有的需要根据数学的逻辑关系和学生的认知规律进行挖掘,这就是教师教学设计的空间和学生数学探究的空间,这对培养学生的数学能力、发展学生的数学素养是必要的, 在节习题、章复习题和阅读、问题与探究等栏目中还设计了一些超过课程标准要求,但与本章内容或章“大背景”相关的进阶性问题、课题或欣赏性材料,目的是为学生打开通向高等数学的一扇窗,在激发对数学学科的持续的兴趣的同时,让学生感受到数学的美,增强对初等数学内容价值、本质的理解.比如,“三角函数”一章的复习题第20题运用泰勒展开的级数说明计算器计算函数值(如sinx,cosx)的原理,对有兴趣的学生来说,此题让他们在了解弧度制的优势性的同时,能够感受到极限的思想、逼近的观念、函数有理化思想等. 从上文可以看出,基于“大背景”的章单元建构框架其实是一种问题解决的建构型教学范式,是在解决由“大背景”产生的大问题的过程中展开数学的研究过程,数学建构的过程也就是数学学习的过程, 综上所述,基于“大背景”的数学教学结构如图1所示.
二、“三角函数”一章的“大背景” 三角函数是刻画周期现象的数学模型,而周期现象是由周期运动引起的,因此,应该选择某种周期运动作为研究的原型,当然,这种原型应该是简单的、基础的,既便于研究,又可以作为刻画复杂的周期运动的基础. 为此,有两种选择,一种是单位圆上运动着的点,另一种是半径为r的圆上运动着的点,前者是后者的特例,考虑到“三角恒等变换”中的基本公式“加法公式”的推导也应该放到这个“大背景”之下进行,而“复合”运动时几个圆的半径可能不同(参见苏教版普通高中课程标准教科书(数学)必修二第10章“三角恒等变换”),我们决定以“半径为r的圆上运动的点”作为本章的“大背景”, 于是,“三角函数”一章的章首语就从周期现象缘自周期运动出发,一个简单的例子是“圆周上一点的运动”,对半径为r的圆,其上一点P可以用(r,α),(r,l)或(x,y)表示(图2),由此提出本章的主问题(大问题):r,α,l,x,y有着怎样的关系?

三、建立本章及相关章节的研究框架 有了上面的“大背景”和“大问题”,只要按照数学研究的基本程序,本章节的内容(中问题)就自然地确定了:
 二、“三角函数”一章的“大背景” 三角函数是刻画周期现象的数学模型,而周期现象是由周期运动引起的,因此,应该选择某种周期运动作为研究的原型,当然,这种原型应该是简单的、基础的,既便于研究,又可以作为刻画复杂的周期运动的基础. 为此,有两种选择,一种是单位圆上运动着的点,另一种是半径为r的圆上运动着的点,前者是后者的特例,考虑到“三角恒等变换”中的基本公式“加法公式”的推导也应该放到这个“大背景”之下进行,而“复合”运动时几个圆的半径可能不同(参见苏教版普通高中课程标准教科书(数学)必修二第10章“三角恒等变换”),我们决定以“半径为r的圆上运动的点”作为本章的“大背景”, 于是,“三角函数”一章的章首语就从周期现象缘自周期运动出发,一个简单的例子是“圆周上一点的运动”,对半径为r的圆,其上一点P可以用(r,α),(r,l)或(x,y)表示(图2),由此提出本章的主问题(大问题):r,α,l,x,y有着怎样的关系?
二、“三角函数”一章的“大背景” 三角函数是刻画周期现象的数学模型,而周期现象是由周期运动引起的,因此,应该选择某种周期运动作为研究的原型,当然,这种原型应该是简单的、基础的,既便于研究,又可以作为刻画复杂的周期运动的基础. 为此,有两种选择,一种是单位圆上运动着的点,另一种是半径为r的圆上运动着的点,前者是后者的特例,考虑到“三角恒等变换”中的基本公式“加法公式”的推导也应该放到这个“大背景”之下进行,而“复合”运动时几个圆的半径可能不同(参见苏教版普通高中课程标准教科书(数学)必修二第10章“三角恒等变换”),我们决定以“半径为r的圆上运动的点”作为本章的“大背景”, 于是,“三角函数”一章的章首语就从周期现象缘自周期运动出发,一个简单的例子是“圆周上一点的运动”,对半径为r的圆,其上一点P可以用(r,α),(r,l)或(x,y)表示(图2),由此提出本章的主问题(大问题):r,α,l,x,y有着怎样的关系?  三、建立本章及相关章节的研究框架 有了上面的“大背景”和“大问题”,只要按照数学研究的基本程序,本章节的内容(中问题)就自然地确定了:
三、建立本章及相关章节的研究框架 有了上面的“大背景”和“大问题”,只要按照数学研究的基本程序,本章节的内容(中问题)就自然地确定了: