《庄子》与艺术真理

      《普通高中数学课程标准（2017年版）》（以下简称《课标》）提出，逻辑推理素养主要表现为掌握推理基本形式和规则，发现问题和提出命题，探索和表达论证过程，理解命题体系，有逻辑地表达与交流[1].逻辑推理包括从特殊到一般的归纳、类比和从一般到特殊的演绎推理.得到数学命题主要依赖于归纳和类比，证明数学命题主要依赖于演绎[2].《课标》第一次明确了归纳推理、类比推理与演绎推理一样，都是有逻辑的思维形式[3].因此，类比推理是培养学生逻辑推理素养过程中不可忽视的内容.然而，类比推理教学的成功案例并不多见，恰当的类比推理教学模式也有待建立[4].尽管HPM专业学习共同体已陆续开发了一系列课例，但这些课例大多属于新授课，在复习课尤其是高三复习课并不多见.众所周知，高三复习课注重知识综合和解题思想方法，注重培养学生分析问题和解决问题的能力.针对高三复习课的特点，要开发较为理想的高三数学课例，将历史上数学家的思想方法融入教学，可能是一条可行的途径.

      为此，笔者对有关类比推理的数学史料进行梳理，从中提炼类比推理的特点，选取合适的素材，在高三复习课中实施类比推理的教学.

      二、类比推理的数学史料研究及其应用

      （一）类比推理的数学史料研究

      1.基于类比推理的数学发现

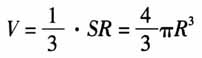      在数学历史上，类比推理是数学家获得数学发现的重要途径.古希腊数学家阿基米德（Archimedes）在《论方法》中写道：“……由圆面积等于以它的周长为底，以它的半径为高的三角形面积这一事实进行推断，我认识到同样应有，球体积等于以球的表面积为底、半径为高的圆锥的体积.”[5]阿基米德通过类比推理，由圆面积与其周长的关系，类比得到球体积与其表面积的关系.因为球的体积公式为，所以球的表面积公式为.

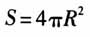      17世纪，英国数学家牛顿（I.Newton）通过类比，得出有理数指数的二项式定理.18世纪，瑞士数学家欧拉（L.Euler）通过将有限次代数方程根与系数的关系类比到无限次方程，解决了“自然数平方倒数和”这一难题[6].19世纪，法国数学家普鲁埃（E.Prouhet）类比三角形的九点圆，发现了四面体的十二点球[7].

      美籍匈牙利数学家波利亚（G.Polya）说过：“类比是一个伟大的引路人.”[8]波利亚在《数学与猜想》《数学的发现》《怎样解题》中对类比推理均有论述.

      在《数学与猜想》和《数学的发现》相关章节中，波利亚列举了许多有关类比推理的习题[9].

      ·证明：若空间两条直线被三个平行平面所截，则相应的截线段成比例（提示：类比较简单的定理）.

      ·证明：平行六面体的四条对角线交于一点，且互相平分（提示：类比较简单的定理）.

      ·证明：三面角中，每两个二面角之和总大于第三个（提示：类比较简单的定理）.

      ·平面几何中有如下定理：“三角形的三条角平分线交于一点，该点是其内切圆的圆心.”类比上述定理，叙述一个立体几何定理.

      ·平面几何中有如下定理：“等腰三角形的底边上的高经过底边中点.”类比上述定理，叙述一个立体几何定理.

      2.类比方向的多样性

      波利亚指出，比较平面几何与立体几何，首先，我们发现平面上的三角形与空间的四面体可作类比.其次，三角形与棱锥可作类比，这两种类比都是合理的，它们各有其价值，在平面几何与立体几何之间有若干类比关系，而不止一个特殊的类比[9].这表明，类比的方向和结论具有多样性.例如，波利亚在《数学的发现》与《数学与猜想》中分别设置了类比勾股定理和海伦公式的问题[10].

      

      

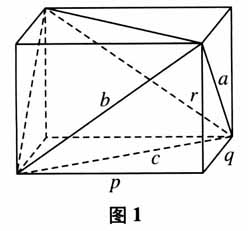      实际上，早在15世纪，意大利艺术大师弗朗西斯卡（P.della Francesca）已经通过类比海伦公式，得到用棱长表示的任意四面体的体积公式[11].18世纪，欧拉又得出了类似的公式.

      3.由类比推理得到的错误命题

      

      （二）类比推理数学史料的应用

      类比推理的相关史料揭示了类比推理创造性、或然性和结论的多样性的特点.阿基米德、牛顿、欧拉等通过类比做出重要发现，体现了类比推理的创造性；阿耶波多、婆罗摩笈多、斐波那契等运用类比推理得出错误结果，体现了类比所得到结论的或然性；波利亚类比勾股定理和海伦公式，得出多个不同命题，说明类比推理的方向具有多样性，类比推理的结果并不是唯一的.