高中数学学科教学承担着传授数学基础知识和基本技能、传递数学基本思想方法,以及在此基础上落实数学学科的立德树人重要任务.而数学学科核心素养则是数学学科育德的具体指标.在进行单课教学设计的过程中,由于课时等问题的限制,教师往往将主要目标放在落实基础知识和基本技能上,而对于学习数学知识背后所承载的培养理性、求真精神等育德价值相对比较忽视.从单课设计的角度来说,会发生上述问题也是有其必然性的.将教学设计的视野仅仅关注在一堂课,势必会削弱这堂课在整个单元中与其他内容时内在联系,而课程标准中的数学学科六大核心素养,作为数学学科立德树人的具体内容,本来也不是一堂课就能够实现的.从课程目标到每一堂课的教学,中间势必需要一个桥梁进行连接,而单元教学设计就起到了这个作用. 笔者以沪教版高二第二学期“复数”的单元教学设计为例进行阐述. 一、设计伊始,明确本单元的主线教学目标指向 单元教学设计可以知识板块作为划分依据,也可以数学思想方法等其他内容作为划分依据.“复数”单元的显性主线是数学知识板块,复数是建构在数系的扩充基础上的,而学生之前学习的内容都是在实数集范围内进行研究的.既然称之为数系的扩充,必然是在原有基础上进行延伸,既要能够解决新的问题,又要保证原有的体系在数系扩充后仍然正确.“复数”单元中的每一个新的概念的提出、新的运算法则的构建,都是在原有基础上的创新,同时又必须保证这些概念与运算的严谨性.所以贯穿“复数”单元教学的隐性主线可以设计为对学生研究数学问题的创新性和严谨性的培养,指向核心素养中的逻辑推理和数学运算. 复数的概念,是在引入虚数单位i的基础上,通过形如a+bi(a,b∈R)的形式来定义的,其实部和虚部都是实数.而之后复数的运算等问题都是通过将问题化归到实部和虚部,通过实数的运算来解决的.而复平面的引入,将复数与复平面上的点以及向量建立了对应关系,复数的部分问题可以转化为几何问题进行研究.将新问题化归到已经掌握的知识内容范畴,是复数单元教学中常见的思想方法,这种思想方法不仅仅在数学问题的研究上很有价值,对于学生日后研究和解决生活中以及其他领域中的问题,也很有借鉴价值.在复数的单元教学中贯穿这一思想,为提高学生的思维品质提供了一条途径. 二、设计过程,注重主线教学目标在课堂中的贯穿 以创新性和严谨性等育德目标作为单元设计的隐性主线,应当尽可能地在本单元的大部分课时中得到体现,借助这一主题的不断反复出现,引起学生的注意,继而形成思维惯性,以达到在通过单元设计落实学科育德任务的目标. 复数的概念,作为本单元的第一课时,在设计时可以充分体现“复数”单元的主线.沪教版教材在这部分内容的处理上采用了直接从复数开方引入虚数单位i的方式.而苏教版、湘教版和人教版教材都在单元伊始介绍了数系的扩充,这对学生理解虚数单位i的引入起到了重要的铺垫作用,关键是对于数系扩充的合理性以及运算的封闭性建立了初步的了解.在处理沪教版教材的第一课时,未必需要向其他教材那样专门用一个课时来进行研究,但是不妨采用在不同数集内解方程的方式,让学生从问题解决的角度审视每一次数系的扩充,理解其背后的创新性和严谨性. 例如:方程x-1=0在自然数集中就有解,而将方程改为x+1=0后,就必须将数系扩充到整数集之后才能有解.继而将方程改为2x-1=0,为了保证方程有解,可以将数系扩充到有理数集.再将方程改为
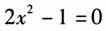
,则必须将数系扩充到实数集后才能有解.所以当我们将方程改成
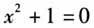
时,涉及了负数开方的问题,学生自然而然地会想到将数系进一步扩充,从而解决新问题,那么虚数单位i的引入,就变得顺理成章.创新性的培养是在一定相关问题研究积累的基础上产生的.在引入了虚数单位i之后是否解决了所有负数开方的问题,是需要提醒学生思考的问题之一.另外,既然是数系的扩充,那么引入虚数单位i之后,构建了复数集是否包含了原有的实数集,也是需要提醒学生关注的问题.继而引申出原来在实数集中的运算,是否也可以扩充到复数集,则可以为单元中复数运算的课时做铺垫. 在进行复数加法和减法的课时设计时,可以继续渗透严谨性的培养.对于复数加法和减法的定义,可以引导学生思考复数的加减法在运算上的封闭性、实数范围内加法的交换律和结合律,推广到复数范围是否还成立等问题,在将问题推广创新的前提下,培养学生的逻辑推理能力,养成思考问题的严谨性.在后期研究复数乘法的课时中,还可以继续就乘法的交换律、结合律以及对加法的分配率是否可以推广到复数范围进行思考,并对整个单元贯穿的创新性和严谨性目标落实进行总结和提升. 除了在课时的设计中可以始终关注单元教学的育德目标落实,创新性和严谨性目标的贯穿还可以落实到作业上.在单课教学设计中,作业关注的重点往往落到知识技能掌握与否,而从单元设计的角度,配合单课短作业,还可以有配套长作业供学生进行研究.例如在课堂教学的基础上,引导学生思考“哪些在实数范围内成立的性质可以推广到复数范围,而哪些不可以推广?其理由是什么?”等问题,就可以设置成单元长作业,在学生进行复数单元学习的时候进行合作研究.通过小组合作等方式,从教材、课外书籍、网络等多渠道获取信息,并在此基础上进行信息加工和小组研讨,形成合作研究的成果.长作业的合作学习,能够给学生更充足的时间对数系扩充问题的创新性和严谨性进一步思考,在小组合作探讨的过程中也能够互相取长补短.
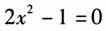 ,则必须将数系扩充到实数集后才能有解.所以当我们将方程改成
,则必须将数系扩充到实数集后才能有解.所以当我们将方程改成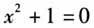 时,涉及了负数开方的问题,学生自然而然地会想到将数系进一步扩充,从而解决新问题,那么虚数单位i的引入,就变得顺理成章.创新性的培养是在一定相关问题研究积累的基础上产生的.在引入了虚数单位i之后是否解决了所有负数开方的问题,是需要提醒学生思考的问题之一.另外,既然是数系的扩充,那么引入虚数单位i之后,构建了复数集是否包含了原有的实数集,也是需要提醒学生关注的问题.继而引申出原来在实数集中的运算,是否也可以扩充到复数集,则可以为单元中复数运算的课时做铺垫. 在进行复数加法和减法的课时设计时,可以继续渗透严谨性的培养.对于复数加法和减法的定义,可以引导学生思考复数的加减法在运算上的封闭性、实数范围内加法的交换律和结合律,推广到复数范围是否还成立等问题,在将问题推广创新的前提下,培养学生的逻辑推理能力,养成思考问题的严谨性.在后期研究复数乘法的课时中,还可以继续就乘法的交换律、结合律以及对加法的分配率是否可以推广到复数范围进行思考,并对整个单元贯穿的创新性和严谨性目标落实进行总结和提升. 除了在课时的设计中可以始终关注单元教学的育德目标落实,创新性和严谨性目标的贯穿还可以落实到作业上.在单课教学设计中,作业关注的重点往往落到知识技能掌握与否,而从单元设计的角度,配合单课短作业,还可以有配套长作业供学生进行研究.例如在课堂教学的基础上,引导学生思考“哪些在实数范围内成立的性质可以推广到复数范围,而哪些不可以推广?其理由是什么?”等问题,就可以设置成单元长作业,在学生进行复数单元学习的时候进行合作研究.通过小组合作等方式,从教材、课外书籍、网络等多渠道获取信息,并在此基础上进行信息加工和小组研讨,形成合作研究的成果.长作业的合作学习,能够给学生更充足的时间对数系扩充问题的创新性和严谨性进一步思考,在小组合作探讨的过程中也能够互相取长补短.
时,涉及了负数开方的问题,学生自然而然地会想到将数系进一步扩充,从而解决新问题,那么虚数单位i的引入,就变得顺理成章.创新性的培养是在一定相关问题研究积累的基础上产生的.在引入了虚数单位i之后是否解决了所有负数开方的问题,是需要提醒学生思考的问题之一.另外,既然是数系的扩充,那么引入虚数单位i之后,构建了复数集是否包含了原有的实数集,也是需要提醒学生关注的问题.继而引申出原来在实数集中的运算,是否也可以扩充到复数集,则可以为单元中复数运算的课时做铺垫. 在进行复数加法和减法的课时设计时,可以继续渗透严谨性的培养.对于复数加法和减法的定义,可以引导学生思考复数的加减法在运算上的封闭性、实数范围内加法的交换律和结合律,推广到复数范围是否还成立等问题,在将问题推广创新的前提下,培养学生的逻辑推理能力,养成思考问题的严谨性.在后期研究复数乘法的课时中,还可以继续就乘法的交换律、结合律以及对加法的分配率是否可以推广到复数范围进行思考,并对整个单元贯穿的创新性和严谨性目标落实进行总结和提升. 除了在课时的设计中可以始终关注单元教学的育德目标落实,创新性和严谨性目标的贯穿还可以落实到作业上.在单课教学设计中,作业关注的重点往往落到知识技能掌握与否,而从单元设计的角度,配合单课短作业,还可以有配套长作业供学生进行研究.例如在课堂教学的基础上,引导学生思考“哪些在实数范围内成立的性质可以推广到复数范围,而哪些不可以推广?其理由是什么?”等问题,就可以设置成单元长作业,在学生进行复数单元学习的时候进行合作研究.通过小组合作等方式,从教材、课外书籍、网络等多渠道获取信息,并在此基础上进行信息加工和小组研讨,形成合作研究的成果.长作业的合作学习,能够给学生更充足的时间对数系扩充问题的创新性和严谨性进一步思考,在小组合作探讨的过程中也能够互相取长补短.