武汉大学机构用户，欢迎您！
从语言的内涵来看，向量语言有表示抽象概念的，如0表示零向量；有表示关系的，如a=-b表示两向量互为反向量；有表示向量运算的，如a·b表示两向量作数量积运算；有表示规律的，如λa=aλ表示实数与向量的积满足交换律.以上诸例体现出向量语言形式的多样性和内涵的丰富性，它是描述向量内容的工具，是向量思想方法建立的载体. （二）向量语言能力 《普通高中数学课程标准（2017年版）》（以下简称《标准》）[1]在课程目标中明确阐述了在学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养，提高从数学角度发现和提出问题、分析和解决问题的能力；同时在主题三“几何与代数”说明中提出，能用向量语言和方法表述和解决数学和物理中的一些问题，发展运算能力和解决实际问题的能力. 《标准》对向量语言能力的要求是非常明确的，而对于利用向量推理论证、运算求解、关系处理、用向量的方法处理实际问题等一系列的与向量有关的能力，必须建立在一定水平的向量语言能力之上，它是形成和提高其他能力的基础和必备条件.向量的语言能力应该包括以下不同的几个方面：①对向量抽象符号意义理解的能力；②对向量语言内涵挖掘的能力；③向量语言的各种形式之间的转化能力；④把向量语言转化其他数学语言的能力；⑤利用向量语言进行推理论证、运算求解的能力；⑥在向量思想方法的指导下利用向量语言解决问题的能力.向量语言能力的形成，有助于对向量知识的理解和深化，有助于学生思维能力的培养和提高，有利于培养学生的数学基本素质. 二、向量语言能力的培养目标 针对向量语言能力的不同侧面，在学生原有知识结构和认知规律的基础之上，向量语言教学应该注重以下几个方面：①了解向量丰富的实际背景，经历从具体问题抽象出向量概念和符号的过程，理解向量符号的内涵，建立符号感；②在实际问题背景中，理解几种向量运算的运算法则、运算律及其几何意义，并能用向量语言的坐标形式进行各种向量运算；③能娴熟地在向量语言的各种形式间相互转换；④能够将向量语言转化为图形、坐标、方程等其他可操作的数学语言，形成语言转化意识；⑤通过向量语言的学习和使用，体会向量语言的简洁性、准确性、多样性及深刻的内涵性和广泛的应用性，从而形成用向量的思想方法思考和解决问题. 三、向量语言能力培养的手段 （一）理解概念内涵，谙熟符号表达 深刻理解概念、法则、规律的内涵，谙熟它们的符号表达形式，是向量语言能力形成和提高的基础及保证.符号以及符号构成的表达式是向量语言的主要表述形式，几乎所有的向量内容都有其固定的符号描述.所以对相关符号的意义的理解是使用向量语言、形成向量语言能力的基础.在教学过程中，应注意以下两个问题. 
②注意形式相近易混淆的向量语言.向量语言中有很多形式相近的内容，在学习过程中必须要在透彻理解有关内容的基础上加以明确区分，若不然肯定会影响语言能力的形成和发展，它往往是阻碍语言能力发展的一个重要的障碍.比如两向量
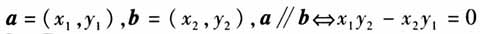，而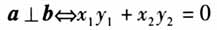
，很多学生容易混淆两种位置关系的等价条件，像这样易混的语言形式应强化区分，以保证向量语言的准确使用. （二）重视向量语言的理解和转化 由于向量语言具有高度的抽象性，所以在具体应用时，必须转化为具体、形象的可操作性语言.这是向量语言能力的关键因素.而转化建立在对向量语言含义有深刻理解的基础之上.以下列举一些向量语言与图形、坐标及方程语言间的常见转化[2].
