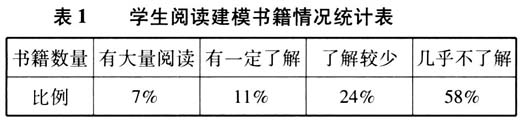
一、问题提出 新课程改革将“数学建模”纳入《普通高中数学课程标准(实验)》[1]中.为了达到“立德树人”的教育目标,新一轮高中数学课程改革聚焦于发展学生的数学核心素养,数学建模素养被列为六大数学核心素养之一.具体描述为:数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、构建模型,求解结论,验证结果并改进模型,最终解决实际问题.数学模型构建了数学与外部世界的桥梁,是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.在数学建模核心素养的形成过程中,学生运用数学知识求解模型,并尝试基于现实背景验证模型和完善模型,积累用数学解决实际问题的经验;能够提升应用能力,增强创新意识. 本研究旨在了解高中学生数学建模意识现状.为此设计了如下研究:根据梳理的数学建模意识相关理论,将数学建模意识划分为数学建模的情感、自信心与价值观、数学建模能力、数学应用意识、分析和逻辑推理能力、创新和发散思维能力、数学化能力,每个维度下都有相应的问题,汇总编制成问卷.本研究的数据资料是将问卷作为主要的研究工具,分析问卷调查结果,阐述作者的看法和论点. 二、调查设计 (一)调查的目的与对象 目的:为了解高中学生数学建模意识现状,落实数学课程标准中对于数学建模素养的培养要求,以我校学生为样本进行问卷调查.以期能更加深入了解学生的数学建模意识,为我校及其他中学数学教学工作者提供教学策略. 对象:为了方便研究,笔者选取了江苏省常州高级中学的高一学生为问卷调查的对象,人数在600人.调查数据真实有效. (二)设计原则 本次调查采用问卷调查方法,设计原则如下: (1)问卷设计目标明确.通过小规模预测,反复讨论、修改等过程,最终形成一份完整问卷,题目表述清晰、数量适中,内容紧扣主题. (2)问卷题目符合学生学情.数学建模问题的选取考虑学生的认知发展和实际生活背景,问卷中设计了以“立体几何”“数列”为背景的问题,尽量贴近我校学生正在学习的内容,以期得到更真实有效的调查结果. (三)问卷的内容设计 参考李明振教授《数学建模认知研究》[2]一书中的数学建模信念问卷、数学建模情感问卷以及数学建模自我监控问卷,以及黎明硕士论文[3]中的问卷并作适当调整改动,设计了《高中生数学建模意识调查》.从数学建模的情感、自信心与价值观、数学建模能力、数学应用意识、分析和逻辑推理能力、创新和发散思维能力、数学化能力等几个维度编制了13道选择题,包括单选题和多选题. 三、结果及分析 在本校高一年级发放并回收有效调查问卷共600份.在同事及一些学生的帮助下,整理数据,形成结果.调查真实有效. 问题1 我了解多少数学建模相关的书籍? 大部分学生接触数学建模书籍数量很少或几乎没有接触.58%的学生表示几乎没了解过建模;24%的学生表示了解较少;18%的学生表示有过大量阅读或有过一定的了解.总的来看,我校高中生对数学建模知识接触较少,差异也较大,需要在今后教学中加大数学建模相关书籍知识的推广,让学生更多了解数学建模及其相关知识.
问题2 你对数学建模感兴趣吗? 表2为学生对数学建模的情感程度统计表,可以看出我校学生对数学建模非常感兴趣和一般感兴趣的人数共占总人数的44%,说明有近一半的学生对数学建模感兴趣;而对数学建模兴趣较少的学生也占总数的近一半,即超半数学生对数学建模不太感兴趣.兴趣是学习研究的源动力,应该通过教师引导、同伴合作,培养学生更多的建模学习兴趣.
问题3 对数学建模的情境的认识(多选题). 84%的学生选择现实问题转化为数学问题;74%的学生选择实际问题转化为数学问题再回归到实际问题;40%的学生选择由一个数学问题转化为另一个数学问题;48%的学生选择将现实问题转化为计算机问题;77%的学生选择由实际问题转化为数学和计算机问题;5%的学生选择其他.大体上,高中学生对数学建模情境有一定的认识,学生都认识到建模情境是由现实问题转化为数学问题或是再回归到实际问题,也可以是一个数学问题转化为另一个数学问题,并且关注到计算机在数学建模中的应用.
问题4 数学建模分为几个步骤? A答案步骤阐述最全面,73%的学生选择答案A(七个);21%的学生选择答案B(五个),在A基础上前后分别减少了模型准备、模型应用两个步骤;5%的学生选择C(四个),在B答案基础上少了模型分析.绝大多数的学生选择A,仅1%学生选择答案D(不清楚),说明只有极少数学生完全不了解建模步骤.
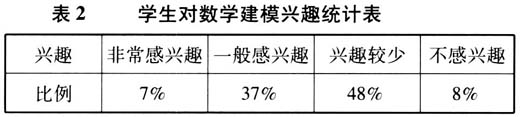
 问题2 你对数学建模感兴趣吗? 表2为学生对数学建模的情感程度统计表,可以看出我校学生对数学建模非常感兴趣和一般感兴趣的人数共占总人数的44%,说明有近一半的学生对数学建模感兴趣;而对数学建模兴趣较少的学生也占总数的近一半,即超半数学生对数学建模不太感兴趣.兴趣是学习研究的源动力,应该通过教师引导、同伴合作,培养学生更多的建模学习兴趣.
问题2 你对数学建模感兴趣吗? 表2为学生对数学建模的情感程度统计表,可以看出我校学生对数学建模非常感兴趣和一般感兴趣的人数共占总人数的44%,说明有近一半的学生对数学建模感兴趣;而对数学建模兴趣较少的学生也占总数的近一半,即超半数学生对数学建模不太感兴趣.兴趣是学习研究的源动力,应该通过教师引导、同伴合作,培养学生更多的建模学习兴趣.  问题3 对数学建模的情境的认识(多选题). 84%的学生选择现实问题转化为数学问题;74%的学生选择实际问题转化为数学问题再回归到实际问题;40%的学生选择由一个数学问题转化为另一个数学问题;48%的学生选择将现实问题转化为计算机问题;77%的学生选择由实际问题转化为数学和计算机问题;5%的学生选择其他.大体上,高中学生对数学建模情境有一定的认识,学生都认识到建模情境是由现实问题转化为数学问题或是再回归到实际问题,也可以是一个数学问题转化为另一个数学问题,并且关注到计算机在数学建模中的应用.
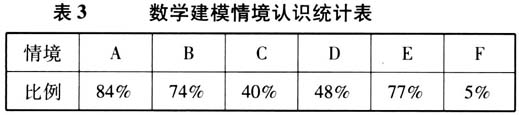
问题3 对数学建模的情境的认识(多选题). 84%的学生选择现实问题转化为数学问题;74%的学生选择实际问题转化为数学问题再回归到实际问题;40%的学生选择由一个数学问题转化为另一个数学问题;48%的学生选择将现实问题转化为计算机问题;77%的学生选择由实际问题转化为数学和计算机问题;5%的学生选择其他.大体上,高中学生对数学建模情境有一定的认识,学生都认识到建模情境是由现实问题转化为数学问题或是再回归到实际问题,也可以是一个数学问题转化为另一个数学问题,并且关注到计算机在数学建模中的应用.  问题4 数学建模分为几个步骤? A答案步骤阐述最全面,73%的学生选择答案A(七个);21%的学生选择答案B(五个),在A基础上前后分别减少了模型准备、模型应用两个步骤;5%的学生选择C(四个),在B答案基础上少了模型分析.绝大多数的学生选择A,仅1%学生选择答案D(不清楚),说明只有极少数学生完全不了解建模步骤.
问题4 数学建模分为几个步骤? A答案步骤阐述最全面,73%的学生选择答案A(七个);21%的学生选择答案B(五个),在A基础上前后分别减少了模型准备、模型应用两个步骤;5%的学生选择C(四个),在B答案基础上少了模型分析.绝大多数的学生选择A,仅1%学生选择答案D(不清楚),说明只有极少数学生完全不了解建模步骤.