当代西方生产性文学批评理论的缘起与问题

      《普通高中数学课程标准（2017年版）》（下称《标准》）指出：“基于数学学科核心素养的教学活动应该把握数学的本质，创设合适的教学情境、提出合适的数学问题，引发学生思考与交流，形成和发展数学学科核心素养.”数学是思维的科学，概念是思维的细胞，概念教学是培养学生数学核心素养的重要载体.本文以北师大版教材“抛物线及其标准方程”教学为例谈谈笔者的做法，不妥之处恳请同行斧正.

      一、教学过程

      环节1 创设情境，引入概念

      情境1 播放PPT让学生欣赏铅球运动轨迹、喷泉、烟花等图片.

      设计意图 让学生了解抛物线几何图形的背景，产生对抛物线的直观感受.

      情境2 问题1：平面直角坐标系中二次函数的图象是抛物线.旋转函数图象，旋转后的抛物线还是二次函数图象吗？究竟什么是抛物线？

      设计意图 概念教学要讲必要性.二次函数的图象旋转后得到的抛物线不一定是二次函数的图象.什么才是抛物线的本质，问题的提出引发了学生探索抛物线概念的渴望.

      情境3 兔子逃跑问题：如图1，一只贪吃的兔子为了吃到更肥美的青草，冒险来到这片危机四伏的草原，好在这里也有避险的地方，一个是右侧的洞穴，一个是左侧的树林.当危险发生时，兔子选择什么样的逃跑路线才能以最快的速度抵达安全地带？本着就近避险的原则，请在草地上作一个边界，使得位于边界一侧的点到树林避险，位于另一侧的点到洞穴避险.

      

      师：这个边界上的点满足什么样的条件？

      生：到洞穴和树林的距离相等.

      师：如果把地面看作一个平面，树林的边界和洞穴可以分别看作什么？这个问题可以转化为一个什么样的数学问题？

      生：一条直线和一个点.可以转化为在平面内找到定点距离和定直线距离相等的点的轨迹.

      师：很棒！要补充说明一下，这个定点是在直线外.

      设计意图 引导学生用数学的眼光观察现象，发现问题.“兔子逃跑问题”来源于动画片，有很强的趣味性，更重要的是它使抛物线概念的生成更加自然，同时也发展了学生的数学抽象和数学建模素养.

      环节2 操作探究，构建概念

      师：我们把这条定直线记作l，定点记作F，请同学们在草稿纸上试着找出一些满足条件的点，看看点的轨迹大致是什么形状.

      （几分钟后）

      生：很难找.除了F到l垂线段中点外，其他的点只能目测，很难准确地画出来，轨迹大致是一条曲线.

      师：为了准确地画出这个轨迹，请拿出我给大家准备的工具（画板、直尺、三角板等）.把直尺固定在画板上当作直线l，把三角板的一条直角边紧靠在直尺的边缘，把细绳（长度与另一直角边相等）的一端固定在顶点A处，另一端固定在画板上钉子（点F）处.用铅笔尖（点M）扣紧绳子，靠住三角板.如图2，你有什么发现？

      

      生：点M到点F及直线l的距离相等，点M在轨迹上.

      师：很好.请同学们将三角板沿着直尺上下滑动，笔尖在画板上描出轨迹的一段.

      （学生四人一组，合作操作）

      师：当三角板下滑到钉子处，下移不动了，怎么办？

      生：把三角板往下翻转，就可以画出下面一段轨迹.

      师：真聪明.根据操作过程，轨迹上半部分和下半部分有什么关系？

      生：关于过点F和直线l垂直的直线对称.

      设计意图 通过合作操作培养学生的团结协作意识，在活动探究中发现轨迹的轴对称特征，让学生体验成功的喜悦.

      师：很好！同学们画出的轨迹是什么形状？

      生：一条向右弯曲的曲线.

      师：为了清晰完整地展现轨迹形状，我们用GeoGebra动画展示作图过程（图3）.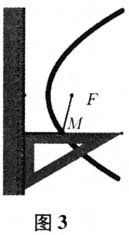

      

      设计意图 动态演示让学生对轨迹有更加直观、精准的认识，为概念的抽象做好充分的准备.

      师：如果将轨迹顺时针旋转90度，像什么曲线？

      生：开口向下的抛物线.

      师：很好，其实轨迹就是一条开口向右的抛物线.根据抛物线的画法，请同学们给抛物线下个定义.

      生：平面内与一个定点F和一条定直线l（l不过F）的距离相等的点的集合叫作抛物线.

      师：用集合语言还可以表示为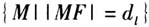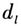，，是M到定直线l的距离.定点F叫作抛物线的焦点，定直线l叫作抛物线的准线.