从代言到行动：教育底层研究的跃迁

      数学概念是思维的基本单位，是数学知识体系中的核心环节，是导出数学定理、法则、公式的逻辑基础，是学生分析问题和解决问题的认知原点，所以概念教学在培育学生核心素养方面有着不可替代的作用.

      数学的生活情境一般性特征，决定了教学中培育学生直观想象素养的必要性.数学概念是在由具体到抽象的过程中形成的，这一过程对学生的认知要求很高，数学概念的直观模型或心理表征可以减轻学生从具体到抽象的学习负担，帮助学生快速建立认知的逻辑通道.

      《普通高中数学课程标准（2017年版）》（以下简称《标准》）指出，直观想象素养主要包括：借助空间认识事物的位置关系、形态变化与运动规律，利用图形描述、分析数学问题，建立数与形的联系，构建数学问题的直观模型，探索解决问题的思路.直观想象是发现和提出数学命题、分析和理解数学命题、探索和形成论证思路的重要辅助手段，是构建抽象结构和进行逻辑推理的思维基础.笔者以指导胡勇老师参加南通市高中青年教师优课评比的“棱柱、棱锥和棱台”一课为例，谈谈如何在概念教学中进行直观想象素养的培育.

      一、课堂实录及思路说明

      （一）设置情境，直观助回忆

      播放生活中各类建筑物图片和空间图形的照片与视频.

      师：生活中有大量空间物体，这些空间几何体是由哪些简单几何体组成的？如何描述和刻画这些简单几何体的形状和大小？构成这些几何体的基本元素之间具有怎样的位置关系？今天，让我们一起来学习立体几何.

      师：研究立体几何还得从平面几何出发，初中阶段，我们学习了平移，谁能告诉我点通过平移后形成什么？

      生：形成线段.

      师：那线段通过平移后形成什么呢？

      生：形成一个平行四边形.

      师：如果将四边形的一条边收缩为一个点，又会形成什么呢？

      生：形成一个三角形.

      师：如果用一条平行于底边的直线去截这个三角形，又会形成什么呢？

      生：形成一个梯形.

      【设计意图】概念教学要从学生熟知的研究方法入手，唤起学生研究的热情.以运动的观点看待平面图形形成的轨迹，以几何直观感知图形的形态与变化，理清知识之间的逻辑关系，形成鲜明而又准确的知觉和表象形象，巩固识图和用图的能力，为后续学习打下基础.

      （二）特征启迪，直观助建构

      师：请同学们想一想，如果将平面图形按某一方向平移，会形成什么？

      教师出示问题，学生陷入沉思，用手比划，但说不出答案.

      活动1：仔细观察下页图1中的几何体，说说它们是由怎样的平面图形平移形成的.

      学生小组开始交流，教师选择小组回答.学生普遍认为图1中的几何体可以由三角形、四边形、五边形、六边形沿某一方向平移而得到.

      

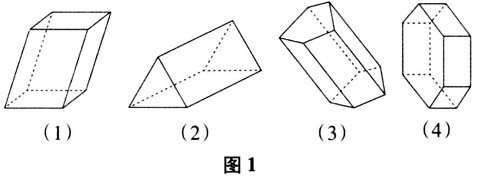      教师用几何画板软件直观验证学生的说法.

      教师给出棱柱的定义：一般地，由一个平面多边形沿某一个方向平移形成的空间几何体叫做棱柱.

      师：棱柱是一个新的概念，请同学们根据定义自主研究它的性质.

      教师出示问题.

      活动2：学生自主阅读教材第5～6页，完成表1.

      

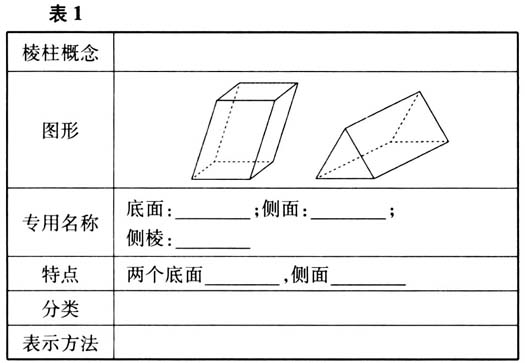      学生自主阅读，小组内部校正，小组代表展示汇报.

      师：同学们对棱柱及有关概念有了一定的了解，下面我们再把它总结提炼一下.

      教师总结：棱柱定义中的关键词是移.两个底面就是平移起止位置的两个面，两个底面是多边形且全等，与对应边平行；侧面是多边形边的移动形成的，侧面是平行四边形；棱是多边形的顶点移动形成的，棱平行且相等.

      学生面露领会的神情.

      师：假如有一个几何体有两个面是全等且平行（对应边平行）的多边形，这样的空间几何体是棱柱吗？

      师：是还是不是，一切用事实说话.教师出示正十二面体模型，如图2所示.

      

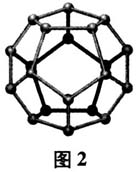      生（摇头）：啊！图2不是.

      师：假如空间几何体有两个面是全等且平行（对应边平行）的多边形，其余各个面是平行四边形，这样的空间几何体是棱柱吗？

      学生议论纷纷，有人说是，有人说不是.

      师：是还是不是，一切以……

      生（笑声一片）：事实说话.

      教师出示两个底一样的斜棱柱拼接而成的几何体，如图3所示.

      

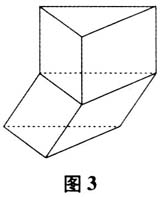      师：是还是不是？

      生（恍然大悟）：不是.

      师：数学概念是精确、简约的，每一个字都有其特定的含义，我们要认真理解概念中的每一个字.

      【设计意图】概念教学要遵循学生的认知规律和思维发展水平，基于认知基础类比设计新知识的生成过程.概念生长于直观材料，借助几何直观和空间想象感知事物的形态与变化，能培养学生运用运动观点和空间想象思考问题的习惯.本部分强调一个移字，促进学生建立了平面几何与立体几何的相互转化的研究方法，通过辨析，想象图形之间的分解与组合，帮助学生加深对概念本质的理解.