马克思的戏仿论探蠡

      数学教学归根结底是数学问题的教学，是学生在数学问题的发现过程、分析过程、解决过程中培养学生数学思维、提升学生数学认知、形成正确的人生观和价值观的育人过程.数学的课堂教学，不仅仅要能培养学生解决问题的能力，还要能够进一步地培养学生提出问题的能力，并能够去设计解决问题的方案，这才是培养人、发展人的科学素质教育.在平时的课堂中，我们的教学往往缺乏问题意识，满足于大容量、快节奏的课堂讲授，以期取得短期的考试分数.殊不知这样的学生在高考的时候，面对熟悉的数学问题能做得熟练，但是因为缺乏问题意识，面临陌生情景就缺乏创新能力，我们的学生往往束手无策.本文中，通过几个案例，谈谈在课堂教学中如何培养学生的问题意识，以期抛砖引玉.

      片段1.在新授课中培养学生提出问题的能力

      新授课中的定义、定理、公式不是一开始就存在于数学家的脑子里的.那些出现在我们教科书中的定义、定理、公式等都是数学家在漫长的认知实践过程中发现并证明的，其过程的艰辛和漫长是我们无法想象的，在我们现在学习的基础上，在数学家们给我们数学结论的基础上，在问题意识的带领下，我们也可以自己动手来发现、探讨一些知识.

      课题1：正弦定理.

      问题1：如图1，小河两岸有A、B两点，在B点所在一侧选择C点，现测得BC长为50m，∠ABC=45°，∠ACB=30°，能由此确定A、B间的距离吗？

      师：谈谈你对这个问题的看法？

      

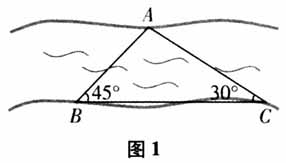      生：由初中的学习我们知道两个条件就可以唯一确定一个直角三角形.上述这个问题其实是在一般的△ABC中，已知角B，C，边a，三角形是唯一确定的，求另一个边c的长.

      师：说得好！对于本题，说说你的想法，你能给其他学生提出什么样的问题呢？

      生：在特殊的直角△ABC中，A，B，C，a，b，c六个量之间有怎样的关系呢？

      

      师：同学们说得非常好.那根据以往数学定理的学习，你又能给同学们提出什么样的问题呢？

      生：特殊的情况推广到一般的时候并不一定都成立，要说明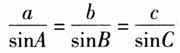在一般三角形中成立的话，一定需要证明，现在需要我们来证明，那应该怎样证明呢？

      问题2：几何画板演示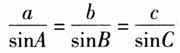在一般的三角形中也成立.你能给出严密的证明过程吗？

      生：化归到直角三角形中来证明……

      师：数学中，一个定理的证明往往会有不止一种方法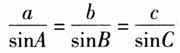，还有其他的证明方法吗？

      片段2.在一轮微专题课中培养学生提出问题的能力

      一轮复习的教学中，大部分时间是基础知识的回顾和习题的讲解.以往的高三数学复习教学中，由于学习过程缺乏问题意识，学生往往处于被动状态，缺少学习的主动性，导致效率不高，失去了本该有的效果，综合能力的提升和数学核心素养的培养更是无稽之谈.在课堂教学中渗透问题意识可以有效落实学生的主体地位，培养学生的创新精神和综合素养，进一步地培养分析问题和解决问题的能力，全面提升学生的综合能力和数学核心素养.

      课题2：涉及多变量的恒成立问题.

      引例：g（（x）=ax-2lnx-a（a∈R，e为自然对数的底数）.任意x∈（1，e]，不等式g（x）＞0恒成立，求a的取值范围.

      师：本题有哪些研究的方法？分别怎样研究呢？

      生：一般地，恒成立问题的研究方法有：分参法，整体最值法，图象法，特殊零点法，化归为命题的否定等方法.注意：解答题不能用图象法研究.

      变题：g（x）=ax-2lnx-a（a∈R，e为自然对数的底数）.存在x∈（1，e]，不等式g（x）＞0成立，求a的取值范围.

      师：本题又有哪些研究的方法？分别怎样研究呢？

      生：一般地，存在性问题研究方法有：分参法、整体最值法、图象法、特殊零点法、化归为命题的否定等方法.解答题一般不用图象法研究.

      问题1：从变量个数、变量类型、函数个数角度对不等式归纳推广，你能提出什么问题呢？

      学生独立思考，生生互相讨论，师生交流.

      生：变量从一个变成两个可以怎样研究呢？函数由一个变成多个可以怎样研究呢？

      生：存在性变量和全称性变量混合在一起可以怎样研究呢？

      师：请根据以上提出的问题，对题目进行改编.