民主真的处于危机之中吗

      2019年12月下旬，某校举行了多媒体教学大赛.其中，数学学科以人教A版《普通高中课程标准实验教科书·数学1（必修）》中的“方程的根与函数的零点”为题，由两位教师进行“同课异构”.笔者有幸受邀参加，并对两位教师的授课情况进行点评.在感叹执教教师高超的语言组织能力和激情澎湃的教学热情之余，笔者陷入思考：在“以学生发展为本”的理念的指导下，青年教师如何才能上好一节课？针对这个问题，笔者结合其中一位执教教师的课例点评，谈谈自身的一些思考，与大家交流.

      一、教学概述与点评

      在不改变原意的情况下，笔者对各教学环节简要概述如下.

      1.课题引入

      上课开始，执教教师用PPT展示课题“方程的根与函数的零点”，并问学生：“课题中哪一个名词你没有见过？”学生回答“零点”.然后，教师提出问题1.

      问题1：判断下列方程的根的个数.

      

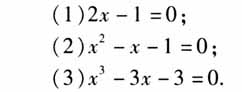      学生通过解方程顺利完成前两道题，但是不知道怎样解决第三道题.这时，教师展示“中外历史上的方程求解”的历史（时间为3分钟左右）.接着又展示了方程lnx+2x-6=0，学生也不知道如何判断这个方程的根的个数.

      俗话说：好的开始是成功的一半.而好的课堂引入往往能够激发学生学习数学的兴趣，勾起学生对要学的内容的好奇心，促进学生满怀期待地投入到新课的学习中去.本节课执教教师精心设计了课题引入：先通过对课题设疑，勾起学生对函数零点的好奇心；然后提出问题1，学生能够解决前两个问题，却解决不了后面两个问题，从而引发学生的认知冲突.因此，这两处都起到了激发学生的求知欲的作用，功能相同，可以去掉一处（当然去掉第一处更合适）.

      在这个环节中，执教教师融入数学史，是一个很好的尝试，值得肯定.然而融入数学史的时机与用时都值得商榷.因为时机不合适不仅会显得课题引入拖沓、不简捷，还会打乱逻辑连贯的教学流程；而用时较长则会挤压本节课重点教学的时间.

      2.函数零点概念的生成

      

      执教教师接着展示问题2.

      问题2：求下列函数的零点.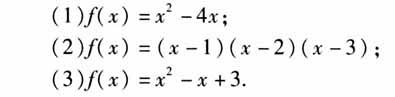

      

      学生通过解方程求出相应函数的零点，教师板书三个等价关系：函数y=f（x）有零点.方程f（x）=0有实根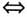函数y=f（x）的图象与x轴有交点.

      概念教学的核心就是“概括”：将凝结在数学概念中的数学家的思维活动打开，以若干典型具体事例为载体，引导学生展开分析各事例的属性、抽象概括共同本质属性、归纳得出数学概念等思维活动而获得概念.因此，概念教学要强调让学生经历概念的概括过程.然而本节课，执教教师仅仅通过一个事例就得到函数零点的概念，缺乏经历从丰富事例中抽象概括出概念的过程，必将导致对零点概念的认识“先天不足”、不深刻.

      问题2是对零点概念的巩固，然而所选取的三个函数均是整式函数，功能类同，如果能把指数函数与对数函数融入其中，就能把前后知识联系起来，完善认知结构.执教教师把“三个等价关系”放在问题2之后，也值得商榷.三个等价关系是零点概念得出后的自然生成，理应放在零点的概念之后.

      3.零点存在性定理的形成

      执教教师用PPT展示探究2.

      探究2：图（略）中是A地某天0～12时气温随时间的变化曲线，然而某同学不小心把4～7时这一段曲线弄掉了.如果该曲线是连续的，那么你能把这段曲线补上吗？

      学生动手画图，教师找两名学生说出作图的情况，总结出曲线在区间[4，7]内的特征（穿过x轴），进而得到f（3）f（8）＜0.于是给出零点的存在性定理，并强调定理成立的两个条件.

      教师接着展示思考.

      思考：（1）如果函数图象不是连续不断的，其他条件不变，结论是否一定成立？

      （2）若函数y=f（x）在区间[a，b]内有零点，一定有f（a）f（b）＜0吗？

      （3）若满足定理条件，函数y=f（x）在区间[a，b]内有几个零点？

      学生先思考，然后教师让学生回答，并适时讲解.

      从教学过程来看，数学定理的教学就是让学生经历从定理的背景中发现和提出猜想、推理论证而获得定理的过程.函数的零点存在性定理也需要让学生经历这样的过程.然而执教教师仅仅给出一个探究（或者讲验证），缺乏必要的猜想，并且从探究中得到的仅仅是定理条件中的“异号”，而对函数图象是否连续也没有强调.何况，对于一般的函数是否也是如此就不得而知了.这样的定理形成过程，必将导致学生对定理内涵的理解出现偏差，应用也将丢三落四.当然，探究2给出的是一个生活事例，放在这里是否合适也值得思考.而对于定理的辨析，也需要从正面、侧面以及反面进行精心设计与打磨.