重新思考比较政治学中的范式演进谱系

      美国著名教育家爱德华兹说过：“教育的伟大目标不只是装饰，应是训练心灵使具备有用的能力，而非填塞前人经验的积累.”课堂教学中教师采用情境教学的方式，能迅速拉近学生与知识的距离，从而提高学生学习的兴趣.但教师对于情境教学的处理，大多是提供对知识的解释，让学生听懂以便于记住，从而认为学生从那里“发现”了知识，这显然是一种误解.抽象的知识只能生成不能发现，而这正是情境教学所欠缺的.现象教学则通过知识、情景、现象的循环，让学生对现象进行思考而形成对世界的认识，这与2017版高中数学课程标准中指出的“三会”是高度一致的.数学抽象产生的硕果就是形成概念，这是数学教学（也是一切教学）的核心之处.

      二、课堂实录与设计意图

      （一）生活现象引入概念

      师：同学们，前面我们学习了平面直角坐标系，它使得平面上的任意一点P都有唯一有序实数对（x，y）与之相对应.比如点（2，-1），可否在坐标系中标注出来？

      （生上前指出点（2，-1）在平面直角坐标系中的位置.）

      师：设想一下，军舰巡逻在北纬38度，东经121度的黄海海面上，如果你是负责观察雷达的哨兵，现在雷达显示前方有一群水雷，你应如何向军舰通报敌情，确定水雷的位置，以便将它们引爆？

      生：如果知道水雷所在的经纬度，便可以确定水雷的位置.

      师：这个其实类似于平面直角坐标系的思维方式，经纬度就相当于点坐标.假设水雷的位置是北纬38.5度，东经120.5度，你能想象两者的相对位置吗？

      生：直接想有点困难.但如果我能在地图上把这两个点标注出来，那么我想我可以发现其相对位置.

      师：好！图1是哨兵观察到的雷达图，你是否有其他方式说出水雷的位置？

      

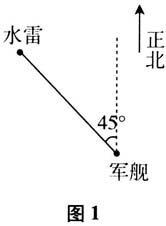      生：水雷在军舰北偏西45°，10海里的位置上.

      师：两种回答，大家觉得哪种更能表现位置的相对性？

      生：后者.听到后面的答案，我在头脑中大概可以浮现出水雷的位置.

      师：经纬度可以标识位置，而这位同学的回答，显示的是两点相对位置关系的刻画.请同学们思考一些，处理这种位置关系中，我们需要考虑哪些要素？

      生：北偏西45°是考虑水雷相对于军舰方位，10海里是考虑军舰与水雷之间的距离.

      师：在军舰位置确定的情况下，根据方位和距离，水雷的位置是否是唯一确定的？

      生：（边比划着图边说）可以的.首先在军舰北偏西45°这样一条射线上，再往前10海里即可发现水雷.

      师：为了更好地体会你所说的两个要素，让我们来实际演练一下.请一个同学站定，演示军舰，那么另外一位同学比划位置，演示水雷所在的位置？

      （演练过程中，有的同学不知道东西南北，就比较困惑，因为要确定方位必须先要确定“北”，再去转换.有些同学比较口语化，报以左多少度，也有和钟表类似的，在10点和11点方向中间.也有同学先考虑北向前10海里，再选择方向变化.）

      生：首先，我们确定正北方向，然后向正西方向旋转45°，再往这个方向向前10海里，从而确定水雷的位置.

      师：好！通过演练，我们进一步明确用方位和距离的两个要素来确定水雷的位置.下面，我们再来看这么一个数学问题.

      设计意图：通过雷达显示水雷位置的处理，通过师生互动，揭示两种表示相对位置关系的方式.通过比对，发现新的位置关系与平面直角坐标系的不同，并抽象出与极坐标系关联的方位和距离两个要素.接下来，教师组织学生活动，在活动中发现问题，并通过对问题的分析、引导、处理，进一步加深学生对这两个要素的理解.确定水雷位置教学情景的应用的分析实现对概念的第一次数学化，这是比较感性的.

      （二）数学现象深化概念

      （投影问题）在平面直角坐标系中，已知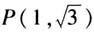点，将点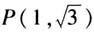绕原点逆时针旋转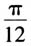，得到点P'，试确定点P'的位置.

      

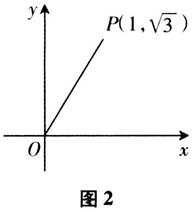      师：大家思考一下，考虑哪些量可以确定点P'的位置？

      生：（思索片刻）点P绕原点逆时针旋转，因此点P'到原点的距离是2.同时由于旋转的角度是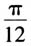，故点P'在一条确定的射线上.