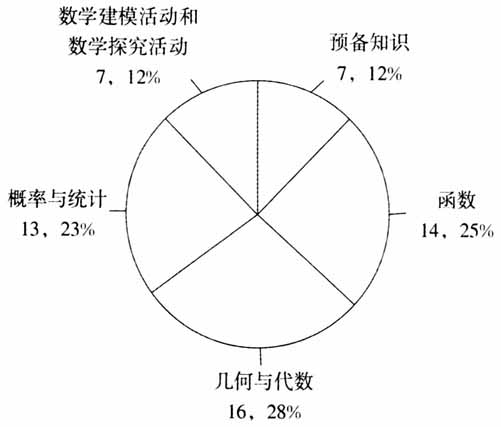
随着数学课程改革的不断深入,数学文化越来越重要.《普通高中数学课程标准(2017年版)》(以下简称《标准》)凝练了学科核心素养,强调将数学文化融入到学习内容中去,开阔学生的数学视野,激发学生的学习兴趣与好奇心,培养学生的科学精神.在此背景下,数学史作为数学文化的重要组成部分也受到了更多的关注.数学史具有丰富的教育价值,包括激发学生的学习兴趣和成就动机,促进学生深刻理解数学,帮助学生形成良好的数学观念等.我国著名的数学家吴文俊院士曾经说过,数学教育和数学史是分不开的.众多研究亦表明,数学史对数学教育有着重要的意义.然而,人们在探讨数学史和数学教育之间的关系时,往往关注教师和学生,较少涉及数学课程.事实上,“数学史融入数学教材”已成为HPM的重要课题.教材是教学的重要载体,是学生获得知识的主要源泉.研究数学史如何融入数学教材有助于促进数学史与数学教材的有机融合,进而有助于教师顺利开展教学活动,有助于学生深刻理解数学知识的本质,提升数学学科核心素养. 本文以入选教育部2019年普通高中国家课程教学用书目录、湖北教育出版社组织专家编写的《普通高中教科书·数学》(以下统称“HEP教材”)必修1、必修2、必修3、必修4,以及选择性必修1、选择性必修2、选择性必修3,共计7本教材中的数学史为例,统计分析HEP教材在数学史总体特征、知识领域、内容分类、栏目分布、呈现方式上的特色,以期更全面、更深刻地认识HEP教材是如何运用和呈现数学史的,并在此基础上对数学史融入数学教材提出相应的建议,以更好地发挥数学史的教育价值. 二、HEP教材中的数学史分析 1.总体特征 首先,考察HEP教材中数学史的内容和总体分布情况.统计发现,7本教材共计使用数学史57次,平均每本教材使用数学史8.14次.其中,必修2的主题为幂函数、指数函数、三角函数等,能够使用的数学史相对较少,仅有5次;而选择性必修2的主要知识为数列、微积分等,具有较为深厚的数学史,所以使用次数最多,为12次.具体情况如下页表1所示. 2.维度分析 (1)知识领域. 研究数学史所属的知识领域,有利于明晰数学知识间的逻辑关系,为教师正确把握数学史内容的教学提供指导,为学生掌握数学知识指明方向,从而促进学生数学学科核心素养的形成和发展.《标准》指出高中数学应突出“函数”“几何与代数”“概率与统计”“数学建模活动与数学探究活动”四大主题,重视数学实践和数学文化.依据《标准》,本文将数学史所属的知识领域划分为:预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动.其中,预备知识包括集合、常用逻辑用语和不等式三部分内容.要确定数学史属于哪一知识领域主要依据数学史的具体内容.例如,选择性必修1中的阅读与讨论“坐标几何史话”属于几何与代数领域,若涉及图片或简介类数学史,则取决于在哪一领域介绍的,如必修1中康托尔和希尔伯特的肖像和简介是在集合中呈现的,属于预备知识领域.HEP教材中数学史所属知识领域统计图如下页图所示. 由图可知,数学史在函数、几何与代数、概率与统计三大领域内的分布总体较为均匀.其中,几何与代数占比最多,函数次之,概率与统计稍低于函数.数学史在几何与代数领域占比最高,这源于几何与代数本身数学史素材比较丰富,包括数系的发展、海伦公式等.但是,HEP教材在选取数学史时有的放矢,较好地把握了这三者的占比关系,并没有出现严重失衡的现象.此外,数学建模活动与数学探究活动中也多次涉及数学史,占比为12%.数学建模活动与数学探究活动旨在培养学生学会用数学的视角发现问题、分析问题、解决问题.在该领域中应用数学史有利于将现实与数学历史融合在一起,促进学生利用数学思维去解决实际问题,进而更好地掌握数学知识,感受数学应用的魅力.

(2)内容分类. 数学史素材丰富多彩,包括数学人物、数学故事、数学问题、数学思想方法等.考察其素材类型,有利于更好地分析数学史内容,发挥数学史的教育功能.本文将教材中的数学史内容分为四大类:数学家及其故事、数学的形成与发展、历史名题猜想和数学的应用.其中,若涉及两者的,则取决于主要内容.例如,“德国数学家康托尔创立了集合论,开辟了进入现代数学的道路”同时涉及数学家和数学的形成,但这句话强调的是集合论的创立,所以将其归为数学的形成与发展.数学史内容分类的具体情况如下页表2所示. 统计表明,HEP教材重视数学史内容选取的丰富性,且较青睐数学的应用.数学应用中蕴涵着丰富的数学思想.在数学应用中渗透数学史可以帮助学生在实际操作中掌握数学方法、体会数学价值,进而使学生加深对数学知识本质的理解,提高其实践能力和创新意识.数学的形成与发展占比为22.8%,高于数学家及其故事的占比,这意味着数学史的选取不再注重数学家及其故事,反而强调知识形成与发展的过程.这是HEP教材对《标准》中数学史要求的积极回应.尽管数学家的故事有助于激起学生的学习兴趣,但其内容相对浅显易懂,很难真正地在学习中促进学生数学能力的提高.相反,关注数学的形成与发展不仅可以让学生体会知识发生、发展的过程,感受数学本身的魅力,而且有利于深化学生对数学发展过程中体现的思想方法的理解与掌握,进而提高其数学能力.以引入复数的概念为例,HEP教材聚焦于数的发展和数系扩充的过程,突出复数的本质特征,深化学生对复数的理解,同时也在开展复数的教学工作中给教师以启发.此外,HEP教材也关注历史名题猜想.在历史名题中解决数学问题,既可以引导学生提升分析问题和解决问题的能力,也可以彰显数学知识经久不衰的魅力,增加学生对数学文化的认同感.

 (2)内容分类. 数学史素材丰富多彩,包括数学人物、数学故事、数学问题、数学思想方法等.考察其素材类型,有利于更好地分析数学史内容,发挥数学史的教育功能.本文将教材中的数学史内容分为四大类:数学家及其故事、数学的形成与发展、历史名题猜想和数学的应用.其中,若涉及两者的,则取决于主要内容.例如,“德国数学家康托尔创立了集合论,开辟了进入现代数学的道路”同时涉及数学家和数学的形成,但这句话强调的是集合论的创立,所以将其归为数学的形成与发展.数学史内容分类的具体情况如下页表2所示. 统计表明,HEP教材重视数学史内容选取的丰富性,且较青睐数学的应用.数学应用中蕴涵着丰富的数学思想.在数学应用中渗透数学史可以帮助学生在实际操作中掌握数学方法、体会数学价值,进而使学生加深对数学知识本质的理解,提高其实践能力和创新意识.数学的形成与发展占比为22.8%,高于数学家及其故事的占比,这意味着数学史的选取不再注重数学家及其故事,反而强调知识形成与发展的过程.这是HEP教材对《标准》中数学史要求的积极回应.尽管数学家的故事有助于激起学生的学习兴趣,但其内容相对浅显易懂,很难真正地在学习中促进学生数学能力的提高.相反,关注数学的形成与发展不仅可以让学生体会知识发生、发展的过程,感受数学本身的魅力,而且有利于深化学生对数学发展过程中体现的思想方法的理解与掌握,进而提高其数学能力.以引入复数的概念为例,HEP教材聚焦于数的发展和数系扩充的过程,突出复数的本质特征,深化学生对复数的理解,同时也在开展复数的教学工作中给教师以启发.此外,HEP教材也关注历史名题猜想.在历史名题中解决数学问题,既可以引导学生提升分析问题和解决问题的能力,也可以彰显数学知识经久不衰的魅力,增加学生对数学文化的认同感.
(2)内容分类. 数学史素材丰富多彩,包括数学人物、数学故事、数学问题、数学思想方法等.考察其素材类型,有利于更好地分析数学史内容,发挥数学史的教育功能.本文将教材中的数学史内容分为四大类:数学家及其故事、数学的形成与发展、历史名题猜想和数学的应用.其中,若涉及两者的,则取决于主要内容.例如,“德国数学家康托尔创立了集合论,开辟了进入现代数学的道路”同时涉及数学家和数学的形成,但这句话强调的是集合论的创立,所以将其归为数学的形成与发展.数学史内容分类的具体情况如下页表2所示. 统计表明,HEP教材重视数学史内容选取的丰富性,且较青睐数学的应用.数学应用中蕴涵着丰富的数学思想.在数学应用中渗透数学史可以帮助学生在实际操作中掌握数学方法、体会数学价值,进而使学生加深对数学知识本质的理解,提高其实践能力和创新意识.数学的形成与发展占比为22.8%,高于数学家及其故事的占比,这意味着数学史的选取不再注重数学家及其故事,反而强调知识形成与发展的过程.这是HEP教材对《标准》中数学史要求的积极回应.尽管数学家的故事有助于激起学生的学习兴趣,但其内容相对浅显易懂,很难真正地在学习中促进学生数学能力的提高.相反,关注数学的形成与发展不仅可以让学生体会知识发生、发展的过程,感受数学本身的魅力,而且有利于深化学生对数学发展过程中体现的思想方法的理解与掌握,进而提高其数学能力.以引入复数的概念为例,HEP教材聚焦于数的发展和数系扩充的过程,突出复数的本质特征,深化学生对复数的理解,同时也在开展复数的教学工作中给教师以启发.此外,HEP教材也关注历史名题猜想.在历史名题中解决数学问题,既可以引导学生提升分析问题和解决问题的能力,也可以彰显数学知识经久不衰的魅力,增加学生对数学文化的认同感.