发生学与结构主义的接合

      高三一轮复习，主要是帮助学生梳理基础知识、训练基本技能、拓展解题思路和方法，深化认识蕴含的数学思想，是基于基础、拾级而上的教学活动.那么如何定位二轮复习的方向、目标？尽管利用微专题进行二轮复习已成为广大教师的共识，也是主要的教学形式.但是微专题教学应用不当，也容易产生轻视概念、就题论题、一言堂、缺少总结的教学问题，事实上，这样的状况屡见不鲜.

      如何提高二轮复习的有效性，寻找科学而又艺术的教学方式？笔者认为二轮复习的定位是：巩固一轮复习成果，完善知识网络，进一步融合数学思想方法体系，提高解决问题的综合性和灵活性.也就是说，二轮复习应重视活动经验的激活与重组，促进有效联想，提高表征问题与转换的能力，勤于反思，从不同的角度认识问题，理解问题本质，提高分析问题和解决问题的能力.本文结合笔者执教的一节研讨课，谈谈自己的思考，不当之处，敬请批评指正.

      一、激活活动经验——促进联想

      学习是经验积累的过程.学生在学习过程中，自主获得了主观性体验和感悟，包括在数学学习的过程中积累起来的数学概念、公式、定理、经验性知识和处理数学问题的常用思想和方法等，把经验转化为直觉的判断，并建立起自己的认知结构，这是学生进一步学习和解决问题的基础.

      遇到一个陌生问题，学生通常的做法是：联想起已经解决的类似的问题，包括题目所涉及教材中的概念、定理、公式、相似问题的解法.这个过程就是激活学生已有的知识经验，促进有效联想.即将新问题的特征与旧问题的特征进行比较，抓住新旧问题的共同特征，将已有的知识和经验与当前问题情境建立联系，利用处理过的类似的旧问题的知识和经验，处理新问题，或把新问题转化为一个已解决了的熟悉问题，从而为新问题的解决做好铺垫.这就像波利亚所说过的：“货源充足和组织良好的知识仓库是一个解题者的重要资本.”而高考题的命制往往又是通过改编教材中的例题、习题等生成，因此重视课本上典型例题和习题，熟悉这些问题的解法，了解它们的变式或延伸，或者解决问题中所蕴含的数学方法，对高考复习也是很有效的.

      【教学片断1】（串讲激活）

      例1 锐角△ABC中，已知sinC=4cosAcosB，则tanAtanB的最大值为________.

      变式：锐角△ABC中，已知sinC=4cosAcosB，则tanA·tanB·tanC的最大值为________.

      学生完成例1和变式后，教师抛出下列问题：

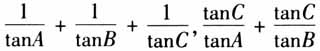      问题1：在上述条件下，怎么求的最小值和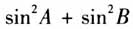的最大值呢？

      设计意图：三角形有着丰富的内涵，其中以正切为背景的三角形最值问题是高考的热点，对学生来说也是难点.利用正余弦定理将题设条件“sinC=4cosAcosB”化成tanA+tanB=4，例1和变式的目标表达式从tanAtanB变式到tanA·tanB·tanC，二元变量到三元变量，对含有tanA，tanB，tanC的式子通过加减乘除等运算进行变形，得到新的目标表达式，不仅可以解决与正切有关的，还可以求与弦有关的目标表达式的最值.学生感悟题目来源，经历变化过程，深化对函数最值求法的认识，为下一步的探究做铺垫.

      问题2：求目标表达式的最值问题一般有哪些方法？（悟一悟）

      师生小结：

      

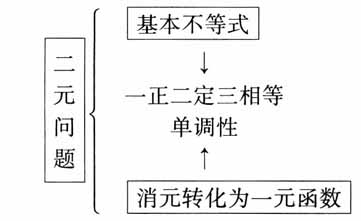      解决例1之后，学生学习热情高涨，教师顺势给出例2.

      【教学片断2】（变式探究）

      问题3：我们还可以从什么角度提出问题？

      生齐答：图形.

      例2 在锐角△ABC中，CD⊥AB，垂足为D，且AD：DB=3：1.在这样的条件下，你能求出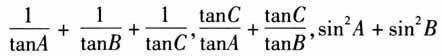的最值吗？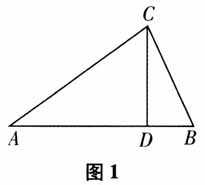

      

      追问：形怎么转化为数量关系呢？

      学生活动：学生根据条件AD：DB=3：1转化为3tanA=tanB，考虑到教学时间有限，仅分析目标表达式的解题方法和思路，不呈现解题过程和结果.

      问题4：刚才我们的已知与目标都是关于角的表达式，那么三角形中研究的对象除了角，还可以研究什么？

      学生活动：学生交流，可以研究三角形的边长、面积、周长、中线长等.

      设计意图：例1从数的角度给出了“tanA+tanB=4”的关系，例2从形出发，学生通过图形分析挖掘出3tanA=tanB.学生不仅可以从代数式结构上进行模式识别，而且建立了几何图形的直观认知.这个环节的重点是让学生感悟不同的表征形式应该如何转换和化简，将新问题转化为熟悉的问题求解.问题2旨在拓宽学生的解题思路，培养学生的发散思维能力.