一、引 言 资本市场是指一年以上融通资金活动的总和,包括股票市场、债券市场和中长期信贷市场 。新中国成立以后,由于种种原因,在很长的一个时期内,我国经济生活中不存在资本市场 ,直到1979年我国政府开始重新发行外债,1981年重新发行内债(到目前国债发行余额已突 破10000亿元人民币,在这期间每年发行的规模也从数十亿元提高到数千亿元),国债市场出 现;1985年国家实行“拨改贷”政策,中长期贷款市场出现;20世纪80年代中期开始,一些 地方出现了企业自发发行的准股票和企业债券,并出现了柜台交易。进入90年代,上海证券 交易所和深圳证券交易所的成立,标志着集中性和有组织的股票市场出现。随后,资本市场 得到快速发展,在我国经济生活中的作用越来越大,关于资本市场的研究也在不断深入,但 资本市场的规模、资本市场的结构、资本市场的效率和经济增长之间的定量关系却没有得到 深入的研究,而它们之间的关系对于我国资本市场健康发展、有效促进经济增长有极其重要 的现实意义。 本文研究采用的一些概念:资本市场的规模可以用长期贷款余额、股票市场的筹资额、债 券发行余额来度量,当然,也有别的衡量方式;[1]资本市场的结构是描述一定时间点中长 期贷款余额、股票市场的筹资额、债券发行余额的比例关系;一般讲资本市场的有效性(Mar ket Efficient)是指资本市场上证券的价格在多大程度上,以什么速度反映了市场上的相关 信息。根据对应信息集的不同,人们将有效市场分为三类:强式有效市场(Strong Efficien cy Market)、半强式有效市场(Semi-strong Efficiency Market)、弱式有效市场(Weak Eff iciency Market)。本文指的资本市场的效率是采用储蓄转化为资本的效率来衡量。 二、文献研究 从古典经济增长理论到现代经济增长理论,都强调资本对经济增长的作用,众多的经济增 长模型都包含着资本这个变量,尽管古典经济增长理论和现代经济增长理论的分析侧重不同 ,比如,古典经济增长理论侧重分析经济增长中土地、资本和劳动交换三个方面,提出储蓄 决定资本积累,进而促进经济增长,但没有分析储蓄转化为资本积累的效率;哈罗德—多马 模型强调储蓄和投资对经济增长的促进作用,索罗模型强调技术进步对经济增长的促进作用 ;现代制度经济学认为,制度变迁的大方向是为了不断减少市场交易费用,使各种资源的所 有者在交易过程中实现自己的行为最大化,与此同时,也使资源流到使用价值最大的当事人 手中,从而推动经济增长。[2]关于资本市场与经济增长的实证研究,国外的经济学家就储 蓄的使用效率问题在美国、德国和日本等主要几个工业化国家进行了一个比较研究,结果表 明美国比日本和德国平均高出三分之一,这主要是由于美国资本市场比较发达,银行体系运 行 效率高。[3]显然,这种研究涉及到了资本市场的效率和经济增长的关系。也有学者研究表 明,间接融资与直接融资之间是互补关系而不是替代关系,尽管从比例来看,两者此消彼 长,但从增长路径来分析,两者是相互依赖和促进的。[4](P28-29)就国内的研究看,主要 是研究资本市场的规模、容量和经济增长的数量关系,采用的方法主要是历史数据拟合的方 法,在拟合过程中假定两者之间的关系为线性关系,如北京大学靳云汇教授、李越博士(注:李越:《资本市场与经济发展的互动关系研究》,北京大学博士后研究工作报告,2000 。), 他们的研究过程中不单独讨论资本市场的效率。[4](P65、93)而且,在确立它们之间的数量 关系时,一般采用典型市场经济国家的资本市场与经济增长的数据。我们认为,典型市场经 济国家的数据不能反映中国转轨经济条件下资本市场与经济增长的数量关系。一些比较权威 的中国宏观经济预测模型中,也不考虑资本市场的规模、结构和效率与经济增长的关系。本 文从中国的实际出发,利用中国资本市场十余年的发展数据,运用比较典型的生产函数来研 究资本市场的规模、结构、效率与经济增长的关系。 三、模型的建立及有关系数的确定 在本文的研究过程中,我们假设中国宏观经济生产函数符合C—D生产函数或AK模型。 1.C—D生产函数的一般形式:

其中:Y表示产出,x[,i],>0,i=1,n;A、a[,i]>0,i=1,n;A是常数,x[,i]是各种投入要素 严格意义上的中国资本市场的数据只有十年左右,用这些数据研究短期增长,技术进步可 以不考虑,在低素质劳动力无限供给的条件下,劳动力也可以不考虑,但体制创新是必须考 虑 的,二十余年的体制改革,对社会生产力有巨大的促进作用,考虑这些因素,中国宏观经济 总产出可以用下述模型来表示:

其中:Y[,t]表示产出,K[,1t]表示股票投入,K[,2t]表示债券投入,K[,3t]表示中长期贷款投入,I[,t]是制度变量(用股票市场的市值与金融资产总价值之比来衡量),a是常数,由于我们引入 了 制度变量可以取消指数系数为正常数的限制,但为了研究问题的简化,假定规模收益不变。 对方程(2)两端取对数得:
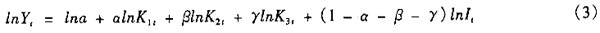
对方程(3)进行变形整理得:
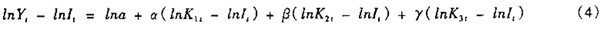
得到新的被解释变量和解释变量。 对新的线性模型进行回归,解释变量强行引入。 回归结果解释:可决系数值为0.999很接近1;调整可决系数为0.996很接近可决系数;通过 总体参数检验,通过F检验。模型各项参数估计均通过单参数t检验,表明各解释变量对被解 释变量具有解释能力,可以引入本模型。 模型参数估计为常数项:3.186、“国债期末余额”:-0.911、“股票筹资累计”:-0.262 、“中长期贷款”:1.895、“制度变量”:0.722。 即有:

 其中:Y表示产出,x[,i],>0,i=1,n;A、a[,i]>0,i=1,n;A是常数,x[,i]是各种投入要素 严格意义上的中国资本市场的数据只有十年左右,用这些数据研究短期增长,技术进步可 以不考虑,在低素质劳动力无限供给的条件下,劳动力也可以不考虑,但体制创新是必须考 虑 的,二十余年的体制改革,对社会生产力有巨大的促进作用,考虑这些因素,中国宏观经济 总产出可以用下述模型来表示:
其中:Y表示产出,x[,i],>0,i=1,n;A、a[,i]>0,i=1,n;A是常数,x[,i]是各种投入要素 严格意义上的中国资本市场的数据只有十年左右,用这些数据研究短期增长,技术进步可 以不考虑,在低素质劳动力无限供给的条件下,劳动力也可以不考虑,但体制创新是必须考 虑 的,二十余年的体制改革,对社会生产力有巨大的促进作用,考虑这些因素,中国宏观经济 总产出可以用下述模型来表示:  其中:Y[,t]表示产出,K[,1t]表示股票投入,K[,2t]表示债券投入,K[,3t]表示中长期贷款投入,I[,t]是制度变量(用股票市场的市值与金融资产总价值之比来衡量),a是常数,由于我们引入 了 制度变量可以取消指数系数为正常数的限制,但为了研究问题的简化,假定规模收益不变。 对方程(2)两端取对数得:
其中:Y[,t]表示产出,K[,1t]表示股票投入,K[,2t]表示债券投入,K[,3t]表示中长期贷款投入,I[,t]是制度变量(用股票市场的市值与金融资产总价值之比来衡量),a是常数,由于我们引入 了 制度变量可以取消指数系数为正常数的限制,但为了研究问题的简化,假定规模收益不变。 对方程(2)两端取对数得: 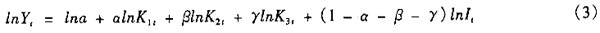 对方程(3)进行变形整理得:
对方程(3)进行变形整理得: 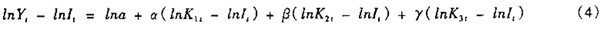 得到新的被解释变量和解释变量。 对新的线性模型进行回归,解释变量强行引入。 回归结果解释:可决系数值为0.999很接近1;调整可决系数为0.996很接近可决系数;通过 总体参数检验,通过F检验。模型各项参数估计均通过单参数t检验,表明各解释变量对被解 释变量具有解释能力,可以引入本模型。 模型参数估计为常数项:3.186、“国债期末余额”:-0.911、“股票筹资累计”:-0.262 、“中长期贷款”:1.895、“制度变量”:0.722。 即有:
得到新的被解释变量和解释变量。 对新的线性模型进行回归,解释变量强行引入。 回归结果解释:可决系数值为0.999很接近1;调整可决系数为0.996很接近可决系数;通过 总体参数检验,通过F检验。模型各项参数估计均通过单参数t检验,表明各解释变量对被解 释变量具有解释能力,可以引入本模型。 模型参数估计为常数项:3.186、“国债期末余额”:-0.911、“股票筹资累计”:-0.262 、“中长期贷款”:1.895、“制度变量”:0.722。 即有: