什么是经济增长？简单地说，就是指一个国家在一定时期内国民财富的的实际增加量或实际增长速度。一般用国内生产总值（GDP ）的增长率、人均国民生产总值（GNP per capita）增长率或人均国民收入（NI per capita）增长率来表示。 随着当今信息时代的发展及未来知识经济时代的迫进，过去主要依靠自然资源、劳动力数量和实物资本积累为经济增长的源泉，现在正逐步转变为以科学技术的进步、制度的创新、人力资本的积累和盘活为经济增长的首要来源。随之而来，教育尤其是高等教育的角色作用，日益成为争论的中心议题。作为科技进步的主要推动力、人力资本投资的主要方式，它对经济增长的贡献，将越来越显著。这种显著性及显著性的大小，需要通过估算的数据来说明。尤其是在我国，一方面希望通过发展高等教育，实现和促进科学技术和社会制度的创新，进而促进经济增长；另一方面由于公共教育资源的稀缺和高等教育产品的平均生产成本日趋递增，人们开始思考高等教育是否应该随着私人教育需求量的扩大而扩大，公共教育资源是更多地投入到基础教育以促进公平，还是更多地投入到高等教育以提高民族的科技竞争力。为了解决这些问题，人们被迫重新去思考和估算，教育及高等教育对经济增长的贡献到底有多大，是否值得进一步扩大高等教育投资。 事实上，人们最初关于教育对经济增长贡献的估算，并不是出于教育自身资源配置效率的原因，而是由于经济学家在寻找导致经济增长的各种因素的时候，发现了教育这个人力资本因素对经济增长的作用，并试图把这种作用分离出来，加以量化，从而开创了估算教育对经济增长贡献的理论和方法。比如前苏联经济学家斯特鲁米林于20世纪20年代所采用的工资劳动简化法，以及美国的经济学家舒尔茨（T.W.Schultz ）、丹尼森（E.F.Denison）于20世纪60 年代创立的关于教育对经济增长贡献的计量方法，都是出于对经济增长因素计量的需要而建立的。本文的目的仅在于综述和发挥各种有关估算教育及高等教育对经济增长贡献的方法。 一、教育贡献率的表示方法 表示教育对经济增长贡献率的方法有多种，概括起来看，可以从估算以下四个方面的指标值入手（注：秦宝庭：《教育与经济增长》，江西教育出版社1992年8月，第81页。）： （1）教育对新增国民收入额的贡献比例， 即由教育所带来的国民收入的增加量（△Y[,e]）占国民收入总增加量（△Y）的比例（△Y[,e] ／△Y）。 （2）教育对国民收入增长速度的贡献比例， 即把教育当作一个生产要素，由教育这个要素投入所带来的那部分国民收入的增长速度（ y[,e]）占国民收入总增长速度（y）的比例（y[,e]／y）。 （3）教育对新增劳动生产率的贡献比例， 即由教育所带来的劳动生产率（劳动力的人均国民收入水平）的增加量（△（Y／L）[,e]）占总劳动生产率增加量（△（Y／L））的比例（△（Y／L）[,e] ／△（Y／L））。 （4）教育对劳动生产率增长速度的贡献比例， 即由教育这一生产要素所带来的劳动生产率的增长速度（S[,e] ）占总劳动生产率增长速度（S[,y]）的比重（S[,e]／S[,y]）。 目前所见到的方法，主要是从前两个方面入手来衡量教育对经济增长的贡献，下面主要介绍前两方面的估算方法。 二、估算教育对国民收入增长额的贡献率的方法 1.舒尔茨的教育投资收益率估算方法 在西方，舒尔茨被认为是就教育对经济增长贡献做定量分析的第一人。（注：（美）Elchanan.柯恩著，王玉昆等译：《教育经济学》， 华东师范大学出版社1989年版，第136页。 ）柯布—道格拉斯生产函数（Cobb—Douglas Production Function ）是西方众多估算方法的根据，也是舒尔茨、丹尼森的估算方法的基础，这里简单介绍一下此函数。 美国经济学家道格拉斯和数学家柯布于20世纪30年代，在研究1899—1922年美国制造业劳动和资本对生产的作用时得出一个生产函数（注：陈璋等：《西方经济理论与实证方法论》，北京大学出版社1993年10月，第185～189页。）。 Y＝AK[α]L[β] 其中，Y代表产出量；K代表资本投入量；L代表劳动投入量；A为不变的“效率系数”；指数α和β代表资本和劳动在总产量中的相对比重，且α＞0，β＞0，α+β＝1。根据美国20 世纪的统计资料估算出α和β分别约为0.25和0.75，表明这一期间，资本所得和劳动所得对总产出的贡献率分别为25%和75%。 参数α和β还可以称之为产出关于资本和劳动的弹性。因为根据柯布—道格拉斯生产函数，存在着资本和劳动的边际产量， 分别为：
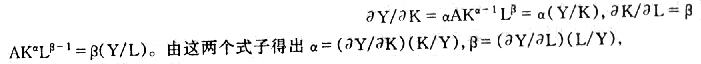
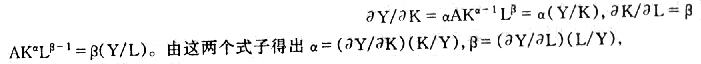α表示产出量的变动率与资本投入量的变动率的比率即产出的资本弹性，β表示产出量的变动率与劳动投入量的变动率的比率即产出的劳动弹性。
