日本企业质量管理方法简介

      MTS（马田系统）的全称为“马赫拉诺比斯·田口系统”，是田口方法中比较新的一个成员。田口博士和他的同事兼高达贰先生于2002年合著了《MTS的技术开发》一书，系统地论述了MTS的基本理论，并介绍了若干应用案例。另外还指出，MTS同“多元控制图”以及“判别分析”之间也有着一定的关联。本文先说明MTS的理论概要，然后就其与SQC方法之间的关联等问题作简要介绍。

      一、MTS概要

      1.MTS的基本观点

      所谓MTS，就是先收集到被视为正常的多元的数据资料，并根据收集的数据确定一个范围作为基准空间，然后对新收集的数据进行判断，如果不在其范围之内，则可判断该数据与先前收集的数据样本之间是不相同的，MTS就是进行这种判断的一系列方法。MT二字缘自马赫拉诺比斯和田口二人的姓氏读音，马氏所创的“马赫拉诺比斯距离”（以下略称为马氏距离）后来被田口方法运用于上述范围的界定。在此，引用兼高达贰先生的“马氏距离的应用——特殊健康诊断例”一文中的典型案例，对MTS的基本考虑方法作一概要说明。

      在某医院，正在进行GOT（谷草转氨酶）和GPT（谷丙转氨酶）等多项关于肝功能的仪器测定。他们对GOT和GPT两个项目分别作了“显示肝细胞功能障碍（因肝炎或中毒性肝功能障碍等而升高）”和“与GOT相同（比GOT对肝脏更具特异性）”的诊断说明。同时对各检查项目分别规定了可视为正常值的范围，例如GOT为2～25（单位），GPT为0～22（单位）。并指出这些标准大多是由仪器厂家和药剂厂家规定好的，现在使用统计方法进行诊断的尝试。具体做法是，首先收集了200名可视为正常人的数据（在该论文中选择发表了其中40名的数据），再根据这些数据绘制成GOT（横轴线）和GPT（纵轴线）的散布图，体现了MTS的基本概念的数据分布情况如图1所示。

      

      图1 MTS的基本概念

      如图（a）所示，首先根据原来收集的数据确定一个可判定为正常值的范围。然后如图中（b）所示，新收集的数据处于上述范围内的判断为正常，凡超出上述范围者则判断为异常。这就是MTS方法的基本概念。本文对于MTS的这一概念只进行概略介绍，但在兼高达贰先生的论文中，由于数据内容涉及人体健康的关系，故详细地介绍了如何判断正常和异常等问题的各种具体考虑方法。

      另外，在MTS方法的背后有着这样一种想法：虽然被认定为正常的数据可以作为一个集来表示，但异常的部分却往往呈现出各种不同的状态。例如，有时GOT和GPT两项都显示偏高，而有时则单独GOT一项出现偏高等等。

      2.MTS的操作步骤

      MTS的操作步骤一般按下列四步实施。

      （1）首先收集上述例子中被认为正常的数据，也就是可作为基准的数据。这种可作为基准的数据集一般称之为基准空间。

      （2）在（1）步骤中所收集的数据基础上，运用“马氏距离”确定可视作属于基准空间的数据范围。

      （3）然后收集不属于基准空间的数据并进行性能评价。在收集和评价过程中，如项目较多时，也可能需要进行项目选择。

      （4）对于新收集的数据，按照其是否处于（2）步骤中所决定的范围之内的实际情况，判断它是否属于来自基准空间的数据。

      二、关于“马氏距离”

      如同图1（a）中散布图所示的GOT和GPT那样，在所测定的项目之间一般存在“相关”关系。在存在某种相关关系的情况下，如按检查项目分别设定范围，则图1（b）中所示的明显与总体不同的A点和B点也可能被判定为正常。所以，在此最好要注意数据出现的频率，考虑整体的范围。对于这种情况的处理，有效的方法就是“马氏距离”。

      1.二元的场合

      

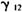      在马氏距离中，如不考虑“相关”因素（即＝0），则可构成下列计算式：

      

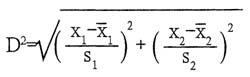      所以，和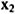将等于基准空间的“欧几里得距离”。另外，马氏距离将出现多元正态分布的概率密度函数的指数部分。由此可知，马氏距离的考虑要同下列情况相对应：对于数据的出现要设想为多元正态分布，在数据容易出现的地方要提高其密度，反之，在数据不易出现的地方要降低其密度。