重思规模：探寻有关“可大可久”之道的政治学

      《辞海》中关于“眼光”的解释是：①眼神，视线.②思想方法、趣味.什么是“数学眼光”呢？数学眼光一般指用数学知识、方法、技能（包括归纳、类比、推理、比较、想象、猜想等数学方法、思想）及数学素养去解决生活、学习中问题的能力，它是一种在掌握了相关数学知识、技能后产生的本能反应，是一种自觉产生的习惯或意识，常见的能力有分析、运算、抽象、化简、符号及图像应用等，数学眼光善于把问题数量化、关系化、符号化、图像化、精准化.因此数学眼光是一种独特的思维，其思维特征具有深刻性、简捷性和广阔性.

      《普通高中数学课程标准（2017年版）》中强调提升学生的核心素养，引导学生会用数学的眼光观察世界.因此在数学课堂教学中，要优化教学活动，有意识地引导学生用数学的眼光来观察问题是关键，笔者就这方面谈一些教学体会.

      一、用数学的眼光进行探究，增强创新意识

      创新是民族发展的需要，增强学生创新意识是数学教学的重要方面.从数学教学的角度看，增强创新意识应当引导学生对数学问题善于质疑，在教学过程中要合理地、有启发性地引导学生质疑、探究，拓展所学的数学知识，让学生在教师引导下，获得更多这方面的体验与感悟，从而培养学生的发散思维和逆向思维，增强学生的创新意识和创新精神.

      以人教A版《数学》（选修2-1）第73页第6题为例，例说用数学眼光进行探究，增强创新意识的一些思路.

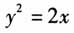      题目：直线y=x-2与抛物线相交于A，B两点，求证OA⊥OB.

      本题主要研究过抛物线顶点的正交弦问题，而且逆命题也成立.很多文章从这两个命题出发进行探究、拓展，基本上从两个维度进行：其一是背景迁移，即将抛物线迁移到椭圆、双曲线中；另一做法是探究拓展这两个命题的一般性结论.在数学杂志中常见上面两种探究，也常见到一些新的结论，但给人感觉创新性不足，怎样做会给人耳目一新的感觉呢？请看2017年高考数学全国卷Ⅰ理科第20题：

      

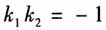      这道高考题创新度较高，考查了直观想象、数学运算、逻辑推理等数学核心素养，充分体现了素养立意的命题要求.这道试题实际上是由上述教材习题的逆命题创新而来，笔者认为该题创新主要体现如下两点：第一，设问创新，以往给出点的坐标，利用待定系数法求曲线方程是常规题，如何跳出俗套，命题人出其不意，利用多给一个点的坐标，把直观想象、数学运算、逻辑推理等数学核心素养巧妙地结合在一起考查；第二，类比创新，研究直线变量中的不变问题，也是常见题，一般情形下类比方法是把两条直线垂直的结论类比为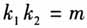（m为常数），在这道考题中，命题人打破常规类比方法，创新为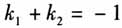，从数学运算角度类比，让人感觉既熟悉又陌生，创新感十足.

      二、用数学的眼光进行概括，培养抽象能力

      一般地，数学概念的形成是数学抽象的过程，例如等差数列、等比数列的定义，导数定义的给出，教材中这些数学概念的抽象方法及过程，对训练、培养学生的抽象眼光当然是很重要的，但是这种方式对学生来说有些被动，我们希望能找到让学生自我发现、主动经历训练数学抽象眼光的素材，使得训练效果更佳.事实上教材中有符合要求的素材，而且还不少，教师应当用心挖掘.例如，在人教A版《数学》（选修2-1）中：

      （1）第41页：设点A，B的坐标分别是（-5，0），（5，0），直线AM，BM相交于M，且它们的斜率之积为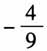，求点M的轨迹方程.

      （2）第55页：点A，B的坐标分别是（-5，0），（5，0），直线AM，BM相交于，且它们的斜率之积为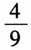，求点M的轨迹方程.

      （3）第42页：点A，B的坐标分别是（-1，0），（1，0），直线AM，BM相交于M，且它们的斜率之商为2，求点M的轨迹方程.

      （4）第74页：点A，B的坐标分别是（-1，0），（1，0），直线AM，BM相交于M，且它们的斜率之差为2，求点M的轨迹方程.

      （5）第81页：点A，B的坐标分别是（-1，0），（1，0），直线AM，BM相交于M，且它们的斜率之和为2，求点M的轨迹方程.

      （6）第80页：已知△ABC的两个顶点A，B的坐标分别是（-5，0），（5，0），且AC，BC所在直线的斜率之积等于m（m≠0），试探求顶点C的轨迹.

      教材中的习题或练习题，都是编者精挑细选后入选的，有相当的代表性，充分挖掘并引导学生领悟其中蕴含的价值，对提升学生数学核心素养大有裨益.这6道练习题如果单独看，可能不易发现它们的隐藏的价值，但是随着学习的深入，教师应当引导学生对这类问题进行总结，它们有太多的共性，为什么要给出6道如此高度相似的题目，想说明什么呢？我们要以什么样的数学眼光来看待它们？

      经过上述质疑，联想教材中椭圆、双曲线定义的推导过程，它们不也是经历归纳共性直至抽象出概念的吗？给学生的启发点到为止，请学生认真探究，希望能得到一些一般性结论.所以教师应当精心使用教材，充分发现、挖掘教材中例题及习题的功能，用好教材，让编者精心选入的素材为我们在培养学生数学核心素养时发挥应有作用.