1969年：艺术体制批判思潮的兴起

      一、基本情况

      （一）授课对象

      学生来自江苏省四星级重点高中，基础较好，有一定的数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析能力.

      （二）教材分析

      所用教材为苏教版《普通高中课程标准实验教科书·数学（选修2-1）》第2章第2.4节抛物线.本节包含两段内容：抛物线的标准方程，抛物线的几何性质.本节课作为节后探究课，侧重对抛物线标准方程中的参数p作进一步探究，旨在对参数p的相关问题进行数学建模.

      教学目标 （1）通过对抛物线标准方程中参数p的探究，理解并掌握与参数p有关结论的发现与求解，提高观察、分析和建模的能力，拓展发散性思维能力和综合概括能力；（2）在对教材经典问题的发散探究中，置身于自主探索、质疑思考的氛围，感悟体验数形结合的思想在解析几何中的应用，不断提升直观想象能力[1].

      教学重点 探究与参数p相关结论的数学模型.

      教学难点 建构对抛物线本质属性的研究路径.

      二、教学过程

      （一）回顾教材，创设情境，引导探究

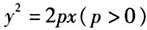      师：同学们，前面我们学习了抛物线的标准方程、抛物线的几何性质等有关知识，请大家回顾一下：在抛物线中，焦点的坐标、准线方程分别是什么？参数p的几何意义是什么？x的系数2p的几何意义又是什么？

      生：焦点坐标为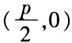，准线方程为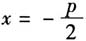，p为焦准距，2p表示通径长.

      师：很好！由此我们发现在对抛物线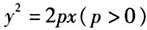的几何性质的研究中，参数p的价值举足轻重，那么我们就一起来对与参数p相关的问题作进一步探究.（教师板书课题）

      

      

      

      

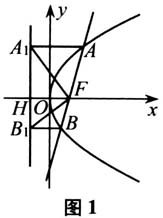
      （二）聚焦p值，发散思考，拓展探究

      

      

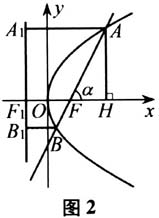      师：同学们对此问题还有其他发现吗？

      生1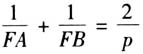：，这又是一个与p相关的定值.

      生2：我发现△OAB的面积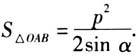

      

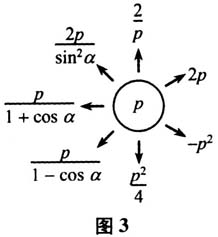      （三）总结提炼，分类思考，升华探究

      师生共同分析，总结提炼，分类思考，凝炼出如下结论：

      

      三、回顾与反思

      （一）教学设计的立意

      新课程倡导教师“用教材”，是要教师以教材为蓝本，对课本中呈现的概念、例题、习题进行科学整合，博采众家之长，设计出立足课本、立足经典的鲜活课例来.这就要求教师要充分研读课本内容，吃透课本精神，把握课本内涵，创造性地使用教材.

      本节课的设计从课本习题出发，以课本问题为依托，结合学情适当整合，展开探究.从这个意义上说，立足课本，自然节约，是一种“原生态”；用足课本，适当拓展，是一种“生成态”；用活课本，焕发活力，是一种“生命态”.通过建构“原生态、生成态、生命态”的三维数学生态课堂，让学生在探究的殿堂中生态化地健康成长.[2]