一、研究背景 (一)地位和作用 复数是中学数学中一个抽象的数学概念,是中学数学学习中不可或缺的一部分.引进虚数,把实数集扩充到复数集,虽然是数学本身的需要,但也只有当复数表示平面上的点这一几何解释出现之后,在解决实际问题中才得到广泛的应用,复数才被人们承认并巩固了下来.复数作为一种新的数学语言,也为我们今后用代数方法解决几何问题提供了新的工具和方法,给数学领域带来了观念性的更新. (二)HPM理论简介 HPM源自于1972年在英国举行的第二届国际数学教育大会(ICME-2)上成立的数学史与数学教学关系国际研究小组(International Study Group on the Relations between History and Pedagogy of Mathematics,简称HPM).HPM关注的内容包括:数学与其他学科的关系、多元文化的数学、数学史与学生的认知发展、数学史与发生教育法、数学史与学生的困难、数学原始文献在教学中的应用等等.HPM研究的最终目的是通过数学史的运用,提高教育教学的水平.数学教育在使学生掌握数学知识、数学思想、培养学生的理性思维方面起着重要作用,数学史对于认识数学与自然界、数学与人类社会的关系,认识数学的科学价值、文化价值方面具有不可替代的作用.在提高数学教育的水平方面,数学史与数学教育相辅相成,不可偏废. (三)数学核心素养简述 在《普通高中数学课程标准(2017年版)》中凝练了学科核心素养的概念,各学科基于学科本质又凝练了本学科的核心素养,明确了学生学习该学科课程后应达成的正确价值观念、必备品格和关键能力.数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学学科核心素养既相对独立,又相互交融,是一个有机的整体. (四)虚数概念的历史 在数学史上,虚数及复数概念的引入经历了一个曲折而漫长的过程,有1300多年,其中充满着数学家的想象力、创造力和不屈不挠的精神. 二、数系的扩充的教学设计片段及设计意图 (一)学情分析 “数系的扩充”是苏教版选修2-2第三章第一节内容.学生从小学到初中已经经历过几次数系的扩充,从最开始的正整数到整数的扩充,再到有理数,再到实数.但是当时由于知识水平和理解水平的限制,对数系扩充并不在意,没有深刻体会数系每一次扩充的历史必然性,不能从知识漫长的曲折艰难的发展过程中体会到人们勇于探索、永不放弃的精神品质. 本节课授课的对象是某县级市四星级高中高一实验班的学生,学生普遍理解力较高,综合能力强,对数学兴趣浓厚,学习目的性明确. (二)教学设计片段 1.设置情境,引入课题 问题1:1545年,意大利数学家卡尔丹(Cardan)在《重要的艺术》一书第37章中,提出了一个问题:把10分成两部分,使其乘积为40.请问怎么分. 学生根据题意列出方程x(10-x)=40,计算Δ<0,于是方程无解. 问题2:为什么Δ<0,方程无解? 生:因为负数不可以开平方. 问题3:为什么负数不能开平方?在什么范围内不能开平方? 生:在实数范围内,负数不能开平方. 设计意图:利用历史上的卡尔丹问题设疑引入,激发学生的好奇心. 2.数系扩充史介绍 问题4:在之前的学习过程中,我们有没有遇到过类似的“数不够用”的问题?请回顾数的学习过程. 学生分组讨论,教师点拨.总结出: (1)在实际生活中,因为计数的需要,产生了自然数,为了表示具有相反意义的量引入了负数,为了测量与分配的需要引入了分数,第一次数学危机人们发现了无理数. (2)在数学发展内部,因为方程x+4=0在自然数中无解从而引进一个新的符号“负号”,产生了负数;因为方程3x+2=0在整数范围内无解,从而引进了一个新的符号“分号”,产生了分数;因为方程
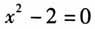
在有理数范围内无解,从而引进了一个新的符号“根号”,产生了无理数. 设计意图:(1)复数是中学课程里数的概念的最后一次扩充,是深化数系理论的很好的素材,虽然它不是重点内容,其定义的理解和复数的应用也是相对简单的,但我们对复数定义的理解常常并不是十分准确,对虚数的产生甚至有同学认为是数学家大脑臆想的产物,也有很多同学甚至老师对虚数的产生仅仅局限于课本上或某些数学书籍中介绍的以下两种说法.其一,虚数系从解方程
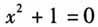
而来,在实数集范围内方程无解,而一旦引入由
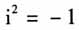
所定义的虚数,此方程就有解了.其二,逆运算常产生新数,减法产生负数,除法产生分数,开方产生无理数和虚数.2003年江苏教育出版社出版的《普通高中课程标准实验教科书·数学》选修2-2中用的就是第一种说法.而实际上虚数的产生是数学发展史上一个重大的事故,上述两种说法只是为虚数的产生提供了可能性,并不是真实的情况,这样就使未接触数学史的人们认为虚数就是这么来的,会引起误解和错解.苏格拉底说:“对真理的追求是永无止境的,我们可能会为自己的梦想放弃一切.”努力培养学生追求真理的坚定信念和无畏精神.
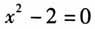 在有理数范围内无解,从而引进了一个新的符号“根号”,产生了无理数. 设计意图:(1)复数是中学课程里数的概念的最后一次扩充,是深化数系理论的很好的素材,虽然它不是重点内容,其定义的理解和复数的应用也是相对简单的,但我们对复数定义的理解常常并不是十分准确,对虚数的产生甚至有同学认为是数学家大脑臆想的产物,也有很多同学甚至老师对虚数的产生仅仅局限于课本上或某些数学书籍中介绍的以下两种说法.其一,虚数系从解方程
在有理数范围内无解,从而引进了一个新的符号“根号”,产生了无理数. 设计意图:(1)复数是中学课程里数的概念的最后一次扩充,是深化数系理论的很好的素材,虽然它不是重点内容,其定义的理解和复数的应用也是相对简单的,但我们对复数定义的理解常常并不是十分准确,对虚数的产生甚至有同学认为是数学家大脑臆想的产物,也有很多同学甚至老师对虚数的产生仅仅局限于课本上或某些数学书籍中介绍的以下两种说法.其一,虚数系从解方程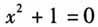 而来,在实数集范围内方程无解,而一旦引入由
而来,在实数集范围内方程无解,而一旦引入由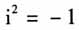 所定义的虚数,此方程就有解了.其二,逆运算常产生新数,减法产生负数,除法产生分数,开方产生无理数和虚数.2003年江苏教育出版社出版的《普通高中课程标准实验教科书·数学》选修2-2中用的就是第一种说法.而实际上虚数的产生是数学发展史上一个重大的事故,上述两种说法只是为虚数的产生提供了可能性,并不是真实的情况,这样就使未接触数学史的人们认为虚数就是这么来的,会引起误解和错解.苏格拉底说:“对真理的追求是永无止境的,我们可能会为自己的梦想放弃一切.”努力培养学生追求真理的坚定信念和无畏精神.
所定义的虚数,此方程就有解了.其二,逆运算常产生新数,减法产生负数,除法产生分数,开方产生无理数和虚数.2003年江苏教育出版社出版的《普通高中课程标准实验教科书·数学》选修2-2中用的就是第一种说法.而实际上虚数的产生是数学发展史上一个重大的事故,上述两种说法只是为虚数的产生提供了可能性,并不是真实的情况,这样就使未接触数学史的人们认为虚数就是这么来的,会引起误解和错解.苏格拉底说:“对真理的追求是永无止境的,我们可能会为自己的梦想放弃一切.”努力培养学生追求真理的坚定信念和无畏精神.