最新的人教A版高中数学教材已于2019年下半年在部分省市正式推行使用,那么,这一版的教材到底遵循怎样的编写思路、与旧版本教材比较到底有什么优点与亮点?我们知道,教材最终是为了服务于学生的学习,为了能够更加客观地解答这两个问题,笔者特意选取了当地两个初三平行班,先让两个班级的学生分别研读新旧两个版本的教材,自学“函数的概念及其表示”这一节课,再通过当场检测反馈自学成效.笔者发现“新教材”班的检测成绩远优于“旧教材”班.为什么会存在这么大的差异?为了了解真相,笔者以学习者的身份对新旧教材中“函数的概念及其表示”这一节内容及其组织形式进行了对比分析,得出的结论是:新教材完全是为学生的自主学习而量身打造的“导航图”,也就是说“不用老师教,学生自己看教材完全能够达成学习任务”. 一、立足单元教学设计理论,明确“学什么” 新教材立足单元教学设计理论,以知识系统为主线将数学中“具有关联性”的知识进行串联、整合、重构形成相对完整的教学模块,在遵循学科自身逻辑特点的基础上不仅为学生提供相对完整的数学认知,而且可以充分发挥单元教学“上挂下联”、贯通上位学科核心素养与下位课时教学目标之间承上启下的优势.当然,不可否认,旧教材在一定程度上也体现了“单元教学设计”的理念,但新教材在单元教学的整体规划与细节处理上更胜一筹. (一)重建初高中关联,深化“衔接”的知识 众所周知,“函数”是高中阶段最抽象、最难学的数学概念之一.旧教材是在“集合”之后,马上进入系统的“函数”模块学习,如此设计显然考虑得“不够周全”:虽然在初中阶段学生学过函数知识,但经过了漫长的“暑期”学习空档期,很多学生已经忘记了什么是函数、函数有什么特点.另外,凭借刚进入高中阶段学生的认知水平,他们能实现函数新定义的顺利构建吗?新教材就“聪明”多了,在“集合”与“函数”之间增加了一章“一元二次函数、方程和不等式”的衔接内容,以学生熟悉的二次函数为着力点与生长点,把初中所学的函数、方程、不等式等知识进行重新关联,并在此基础上掌握“基本不等式”模型,学会“一元二次不等式”的解法,为后续学习函数模块提供必要的知识与技能储备. (二)舍弃无关内容,攻克“核心”的知识 “映射”从最早与函数“平起平坐”,到跻身于教材“角落一隅”,到最后被“边缘化”.尽管“映射”的地位如此尴尬,但前面几个版本的教材都没有把这部分内容删去,似乎保留“映射”概念有助于理解“函数是一种特殊的映射”,但这次新教材却完全抹去了“映射”及相关内容.对于“函数的概念及其表示”一节来说,其核心知识就是函数概念的本身,即如何通过具体的实例抽象出“集合说”这一函数定义的表述形式,并在此基础上进一步理解函数的“三要素”与“表示方法”.既然函数概念的建构与“映射”不存在直接的“关联性”,舍弃“映射”反而有助于凸显学习目标,从而从根本上解决了困扰一线教师多年的“函数概念教学中‘映射’上还是不上”的问题.当然,学生有了函数的认知基础,如果以后再学习“映射”也是水到渠成的事. 二、立足学习动机理论,唤起学生“我要学” 学习动机就是发动和维持个体学习活动,并使之朝向一定目标的内部动力机制,是直接推动学生学习的内部动因,学习动机的缺失或者激发不足会直接影响学习的效果与进程.旧教材也关注到了学习动机的作用,但更多是指向“外部学习动机”.在“函数的概念及其表示”一节,旧教材是这样唤起学生学习动机的:“在初中我们已经学习过函数的概念,并且知道可以用函数描述变量之间的依赖关系,现在我们将进一步学习函数及其构成要素……”,也就是说“初中函数没学完,在高中还要继续学”,其言外之意是“学习函数是函数概念发展的需求”.但很多学生可能会有这样的疑惑:“初中对函数的概念表述已经很明确,为何还要继续学习”“学了函数到底有什么用”……这些困惑如果得不到有效解答就会直接制约学生的学习欲望.因此,以“数学发展的需求”的外部因素来唤起学生学习动机显然很难达成预期的效果,充其量只是为“让我学”呐喊助威. 新教材以学生自身发展的内在需求为学习动机的发力点,竭尽所能从内心深处激发学生强烈的学习欲望.同样是“函数的概念及其表示”一节的概念引入,新教材是这样描述的:正方形的周长l与边长x的对应关系是l=4x,而且对于每一个确定的l都有唯一的x与之对应,因此l是x的函数,这个函数与正比例函数y=4x相同吗?又如,你能用已有的函数知识判断y=x与
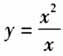
是否相同吗?对照初中阶段对函数定义的表述,学生很难作出准确判断,相当于从侧面告诉学生“初中的函数定义是不完善的或者说对函数的本质属性揭示的还不够,必须要进一步学习”.新教材通过这两个触及学生认知“短板”的问题,引发了学生认知上的冲突,从而激发了学生“我要学”的欲望. 三、立足问题链教学理论,指导“如何学” 新旧教材中都包含了相当数量的“思考”与“提示”性的问题,但最大的区别是:旧教材大都呈现的是一个个相对孤立的问题,而新教材呈现的往往是一组组有中心、有序列、相对独立而又相互关联的问题链.问题链不仅可以为学生提供数学学习的骨架,使学生经问题链获得较高水平的数学知识,而且问题链中问题间的跨度又为学生的高水平思维提供了无限的可能[1]. (一)以问题链搭建思维阶梯 在函数概念的生成环节中,旧教材先给出了“炮弹飞行距离”“臭氧层空洞”“恩格尔系数”这3个独立的、分别暗含函数“解析式、图像、表格”这3种表示形式的生活实例,然后直接提出“分析、归纳以上3个实例,它们有什么共同点”——没有任何铺垫性的提示,对学生来说想要发现“共同点”是多么的困难,即使发现了“共同点”,如何借助“共同点”来提炼函数定义的一般表述更是难上加难.
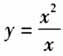 是否相同吗?对照初中阶段对函数定义的表述,学生很难作出准确判断,相当于从侧面告诉学生“初中的函数定义是不完善的或者说对函数的本质属性揭示的还不够,必须要进一步学习”.新教材通过这两个触及学生认知“短板”的问题,引发了学生认知上的冲突,从而激发了学生“我要学”的欲望. 三、立足问题链教学理论,指导“如何学” 新旧教材中都包含了相当数量的“思考”与“提示”性的问题,但最大的区别是:旧教材大都呈现的是一个个相对孤立的问题,而新教材呈现的往往是一组组有中心、有序列、相对独立而又相互关联的问题链.问题链不仅可以为学生提供数学学习的骨架,使学生经问题链获得较高水平的数学知识,而且问题链中问题间的跨度又为学生的高水平思维提供了无限的可能[1]. (一)以问题链搭建思维阶梯 在函数概念的生成环节中,旧教材先给出了“炮弹飞行距离”“臭氧层空洞”“恩格尔系数”这3个独立的、分别暗含函数“解析式、图像、表格”这3种表示形式的生活实例,然后直接提出“分析、归纳以上3个实例,它们有什么共同点”——没有任何铺垫性的提示,对学生来说想要发现“共同点”是多么的困难,即使发现了“共同点”,如何借助“共同点”来提炼函数定义的一般表述更是难上加难.
是否相同吗?对照初中阶段对函数定义的表述,学生很难作出准确判断,相当于从侧面告诉学生“初中的函数定义是不完善的或者说对函数的本质属性揭示的还不够,必须要进一步学习”.新教材通过这两个触及学生认知“短板”的问题,引发了学生认知上的冲突,从而激发了学生“我要学”的欲望. 三、立足问题链教学理论,指导“如何学” 新旧教材中都包含了相当数量的“思考”与“提示”性的问题,但最大的区别是:旧教材大都呈现的是一个个相对孤立的问题,而新教材呈现的往往是一组组有中心、有序列、相对独立而又相互关联的问题链.问题链不仅可以为学生提供数学学习的骨架,使学生经问题链获得较高水平的数学知识,而且问题链中问题间的跨度又为学生的高水平思维提供了无限的可能[1]. (一)以问题链搭建思维阶梯 在函数概念的生成环节中,旧教材先给出了“炮弹飞行距离”“臭氧层空洞”“恩格尔系数”这3个独立的、分别暗含函数“解析式、图像、表格”这3种表示形式的生活实例,然后直接提出“分析、归纳以上3个实例,它们有什么共同点”——没有任何铺垫性的提示,对学生来说想要发现“共同点”是多么的困难,即使发现了“共同点”,如何借助“共同点”来提炼函数定义的一般表述更是难上加难.