数学建模是指对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题.即在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题.为了延伸建模教学的效果,进一步培养学生数学建模与探究实验的能力和素养,教师鼓励学生进行课外研究:寻找生活中两个变量做一个统计调查,分析它们的相关性,并提出自己的看法或建议,写成建模论文.撰写建模论文是一种研究性学习有意义的尝试,可以锻炼学生发现问题、解决问题的能力.建模论文突出三个问题:用什么模型,解决什么问题;通过怎样的思路来解决问题;最后结果怎么样. 中国人口众多,其中学校是人员密集的场所之一.在发生紧急突发状况时(如地震、火灾),如何科学、有序、快速地安排各楼层学生和教师疏散,杜绝人员伤亡,是非常重要紧迫的课题.云南省位于地震带上,是地震多发省份,昆明常受地震波及,做好应急疏散演练有很强的现实意义.因此,引导学生基于线性回归知识对昆明滇池中学应急疏散行为进行预测研究,并对模型进行验证,同时对疏散方案提出优化意见,可以为应急疏散和救援工作提供数据支持,也为学校修订和完善目前的疏散方案提供数据支持. 一、问题的提出 滇池中学教学楼共五层,其中二至四层每层共有36间教室,加上五层一间,总共37间教室,每间教室里的学生可以沿“过道—楼梯间”走到一楼.由此完成下面问题: (1)用数学模型来分析这栋楼学生撤离所需时间;(2)根据建立的模型选择最佳撤离方案. 二、模型假设 (一)疏散原则 本文确定的疏散原则为:楼层低的年级先疏散、离楼梯口近的班级先疏散.这一疏散原则符合国际惯例,以提高救援效率为出发点和落脚点. (二)应急疏散线性回归模型的构建 本文做如下假定: (1)紧急突发情况发生时,学生和教师跑步从教室至操场疏散,每个班人与人间隔的时间相同; (2)每部楼梯可同时疏散的人员总数不做限定,一个楼层的人员全部疏散完毕后再疏散高一楼层的人员; (3)影响疏散的其他因素均不考虑.根据学校实际情况,统计数据“各楼层人员分布情况”“各楼层楼梯分流人数和时间统计表”. 三、问题分析 事实表明,紧急情况发生时,教室所在楼层的高低以及教室距离楼梯的远近是影响撤离时间长短的重要因素.而各个班级因人数差距不大,就不会对疏散时间产生大的影响.因此,对每层楼每部楼梯的撤离人数和时间分别构建数学模型,分别研究变量关系是更为合理的做法. (一)对每个楼层的疏散情况构建回归模型 昆明滇池中学每层楼都设置了三部楼梯,若选取每部楼梯疏散的人数为自变量x,疏散时间(出教室并经过楼梯到达一楼的时间)为因变量y,作散点图(图1).可从图中看出,样本点呈条状分布,每部楼梯疏散的人数和撤离时间有比较好的线性相关关系,因此可以用回归直线
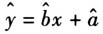
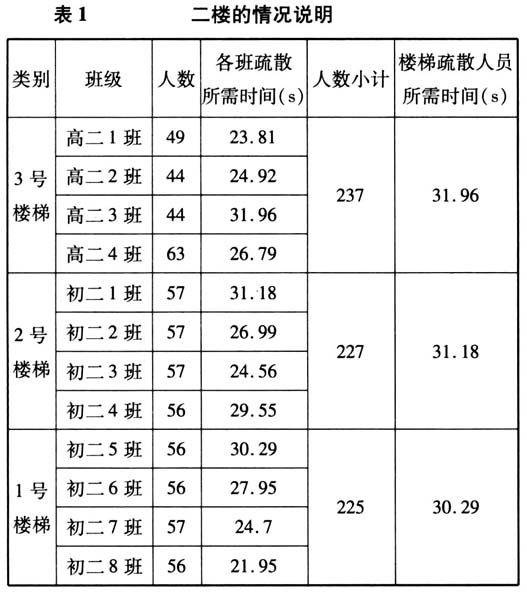
来近似刻画它们之间的关系.如二楼的回归模型情况说明如表1所示,散点图如图1.
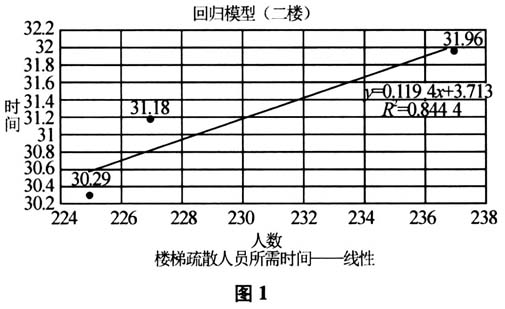
上述是以现有疏散方案为基础进行的分析,经过观察发现,该方案存在如下问题:每部楼梯分流的总人数并不均衡,3号楼梯703人,2号楼梯736人,1号楼梯680人.如果把二楼的初二4班的56名学生分两部分,28人走2号楼梯,另28人走1号楼梯,则每部楼梯总分流的人数将变得均衡,分别为3号楼梯703人,2号楼梯708人,1号楼梯708人. (二)对二楼方案优化后重新构建回归模型 优化后的回归模型情况说明如表2,散点图如图2.
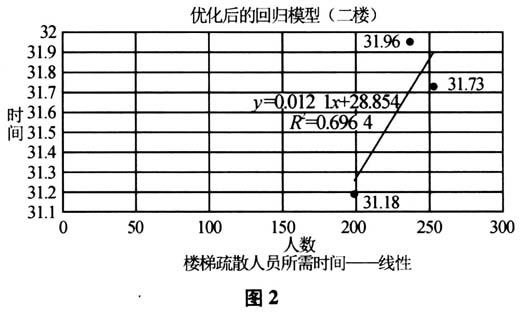
四、对回归模型的验证及相关运用 (一)将现有疏散方案进行优化 由统计数据及预测可以得出,在经过各楼梯口人数优化后,回归方程斜率及纵截距均发生变化,斜率数值较之前有所减小.经过前文分析可知,目前对二楼的疏散方案进行了优化,取楼梯最大疏散人数315人(班级人数按63人计,每部楼梯5个班)代入回归方程中检验,得出优化前41.32s,优化后32.67s,有明显优化效果.以地震为例,在距离震源中心500km时大约有一分钟的逃生时间,而大地震来临时通常只有15s时间逃生.以此优化后,井然有序撤离时可节约近10s的逃生时间,进而大大提高生还的可能性.
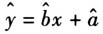 来近似刻画它们之间的关系.如二楼的回归模型情况说明如表1所示,散点图如图1.
来近似刻画它们之间的关系.如二楼的回归模型情况说明如表1所示,散点图如图1. 
 上述是以现有疏散方案为基础进行的分析,经过观察发现,该方案存在如下问题:每部楼梯分流的总人数并不均衡,3号楼梯703人,2号楼梯736人,1号楼梯680人.如果把二楼的初二4班的56名学生分两部分,28人走2号楼梯,另28人走1号楼梯,则每部楼梯总分流的人数将变得均衡,分别为3号楼梯703人,2号楼梯708人,1号楼梯708人. (二)对二楼方案优化后重新构建回归模型 优化后的回归模型情况说明如表2,散点图如图2.
上述是以现有疏散方案为基础进行的分析,经过观察发现,该方案存在如下问题:每部楼梯分流的总人数并不均衡,3号楼梯703人,2号楼梯736人,1号楼梯680人.如果把二楼的初二4班的56名学生分两部分,28人走2号楼梯,另28人走1号楼梯,则每部楼梯总分流的人数将变得均衡,分别为3号楼梯703人,2号楼梯708人,1号楼梯708人. (二)对二楼方案优化后重新构建回归模型 优化后的回归模型情况说明如表2,散点图如图2. 
 四、对回归模型的验证及相关运用 (一)将现有疏散方案进行优化 由统计数据及预测可以得出,在经过各楼梯口人数优化后,回归方程斜率及纵截距均发生变化,斜率数值较之前有所减小.经过前文分析可知,目前对二楼的疏散方案进行了优化,取楼梯最大疏散人数315人(班级人数按63人计,每部楼梯5个班)代入回归方程中检验,得出优化前41.32s,优化后32.67s,有明显优化效果.以地震为例,在距离震源中心500km时大约有一分钟的逃生时间,而大地震来临时通常只有15s时间逃生.以此优化后,井然有序撤离时可节约近10s的逃生时间,进而大大提高生还的可能性.
四、对回归模型的验证及相关运用 (一)将现有疏散方案进行优化 由统计数据及预测可以得出,在经过各楼梯口人数优化后,回归方程斜率及纵截距均发生变化,斜率数值较之前有所减小.经过前文分析可知,目前对二楼的疏散方案进行了优化,取楼梯最大疏散人数315人(班级人数按63人计,每部楼梯5个班)代入回归方程中检验,得出优化前41.32s,优化后32.67s,有明显优化效果.以地震为例,在距离震源中心500km时大约有一分钟的逃生时间,而大地震来临时通常只有15s时间逃生.以此优化后,井然有序撤离时可节约近10s的逃生时间,进而大大提高生还的可能性.