公有制印记与改制家族企业的内部社会责任

      教育是一个由多种要素组成的庞大系统，其系统内部各要素的吻合或匹配对教师教学及学生学习具有积极的促进作用.[1]一致性分析范式是指判断、分析课程系统各个要素之间吻合程度的理念、程序与方法的总和.[2]2001年《基础教育课程改革纲要（试行）》指出：国家课程标准是教材编写、教学、评估和考试命题的依据，是国家管理和评价课程的基础.[3]自此，我国学者开始关注课程标准与诸多教育要素的一致性问题，并在理论和实践层面进行探索.

      理论层面主要以介绍国外研究工具为主，如张雨强详细介绍了韦伯模式[4]，杨玉琴重点分析Achieve工具的分析框架及应用过程[5]，刘学智对3种典型的一致性研究工具做出了本土化的分析[6].实践层面主要是对国际上盛行的韦伯模式、SEC模式和Achieve模式的运用，如刘恩山运用SEC模式分析2010年高考生物试卷与课程标准的一致性[7]，焦传玲运用韦伯模式分析高考化学试题与课程标准的一致性[8]，刘学智将韦伯模式与质性研究结合分析小学数学期末检测试卷与课程标准的一致性[9]，郝婕运用SEC模式分析初中数学教学与学生认知水平的一致性[10].

      高考数学试题与课程标准之间的一致性研究一直备受关注，但《普通高中数学课程标准（2017年版）》（下文简称课程标准）颁布后，分析其与高考试题一致性的研究尚不多见.为此，笔者对2019年高考数学全国卷I（含理科、文科）进行研究，选取韦伯一致性分析模式框架，从知识种类、知识深度、知识广度、知识分布平衡性4个维度，分析高考数学试题是否遵循课程标准关于“命题应依据学业质量标准和课程内容，注重对学生数学学科核心素养的考查，处理好数学学科核心素养与知识技能关系”[11]的原则.

      一、研究设计

      （一）研究对象与工具

      本文选取韦伯一致性分析模式的框架，从知识种类、知识深度、知识广度、知识分布平衡性[2]这4个维度考查2019高考数学全国卷I与课程标准的一致性.一致性判断标准及可接受水平见下页表1.

      （二）课程标准与高考数学试题一致性分析的编码统计

      （1）对课程标准的编码统计

      我国高中数学知识涉及5大知识模块，每个模块分为不同的主题，具体如下页表2所示.高中数学课程分为必修课程、选择性必修课程与选修课程.本文只研究必修课程、选择性必修课程的知识模块.故2019年高考数学全国卷I理科与文科卷中的选考题第22、23题不作为本文研究的内容.

      

      

      （2）对高考数学试题的编码统计

      在编码中，以每道题目所涉及的知识模块为研究对象，其中选择题、填空题、解答题涉及2个知识模块，则记为2个题目.例如，全国卷I文科第10题涉及平面解析几何与三角函数，分别属于几何与代数、函数模块，故记作2道题目.全国卷I理科高考试题编码结果如下：预备知识模块有3道题，函数知识模块有11道题，几何与代数知识模块有11道题，概率与统计知识模块有4道题，数学建模与数学探究活动知识模块有2道题，综上，全国卷I理科高考试题总数为31个.全国卷I文科高考试题编码结果如下：预备知识模块有5道题，函数知识模块有12道题，几何与代数知识模块有10道题，概率与统计知识模块有3道题，数学建模与数学探究活动知识模块有1道题，综上，全国卷I文科高考试题总数为31个.具体试题编码如例1所示.

      例1：（2019全国卷I理科第19题）已知抛物线C：y2=3x的焦点为F，斜率为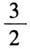的直线l与C的交点为A，B，与x轴的交点为P.

      （1）若｜AF｜+｜BF｜=4，求l的方程；

      （2）若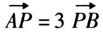，求｜AB｜.

      本题属于几何与代数知识模块，涉及的知识种类为“了解抛物线的定义、几何图形和标准方程”“了解抛物线的简单应用”“会用向量方法解决简单的平面几何问题”共3条课程标准中的具体内容要求.该题符合课程标准中“会用向量方法解决简单的平面几何问题”的内容深度要求，高于“了解抛物线的定义、几何图形和标准方程”“了解抛物线的简单应用”的内容深度要求；涉及运用抛物线的性质等相关知识点解决问题，高于“了解”的认知水平.学生解决问题过程中所运用的知识点与课程标准内容要求期望学生所要学习的知识范围吻合，可见该试题与课程标准的内容广度一致性较高.