武汉大学机构用户,欢迎您!
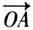 =a,
=a, =b,则∠AOB=θ(0°≤θ≤180°)叫作向量a与b的夹角”,“已知两个非零向量a,b,我们把数量|a||b|cosθ叫作a与b的数量积(或内积)……我们规定:零向量与任一向量的数量积为0”,“设a和b都是非零向量,则a⊥b
=b,则∠AOB=θ(0°≤θ≤180°)叫作向量a与b的夹角”,“已知两个非零向量a,b,我们把数量|a||b|cosθ叫作a与b的数量积(或内积)……我们规定:零向量与任一向量的数量积为0”,“设a和b都是非零向量,则a⊥b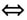 a·b=0”……蹊跷的是,既然向量有方向,为何从不提及零向量的方向?两个非零向量有夹角,那么零向量与任一向量的夹角如何定义?规定零向量与任一向量平行且数量积为0的合理性体现在哪?既然规定零向量与任一向量平行,那么能规定零向量与任一向量垂直吗?这样的疑惑不只是笔者有,笔者曾查阅十来年的期刊,其中的一些观点截然相反.直到笔者读到人教A版教材副主编章建跃博士刊发在《中小学数学(高中版)》2010年第9期上的《把精力集中在核心知识的研究上》一文: “在向量代数中,我们感兴趣的是向量的运算及其规律,而且首先是非零向量,因为它们有好的运算——加法,并由此延伸出数乘向量.为了使它的逆运算(即减法)完满、不留空白,必须引进零向量.这是零向量的核心意义,就像实数集中的0在运算中的地位一样.由于零向量的位置特殊,数学家们约定‘零向量的方向不确定’.这样,在处理问题时,可根据需要让零向量与某一向量平行或垂直.这是一种人为的、合乎习惯的并且方便于应用的规定……” 读到章建跃博士关于零向量方向的这份“终审判决”,笔者才算认清了事实的真相,而且章博士还精准地定位了零向量的核心价值,让笔者清楚地理解了教材编写的思路.在查阅资料中笔者还发现,苏教版教材对零向量的处理方式与大纲版教材和人教A版教材相同,而人教B版教材、北师大版教材、湘教版教材及多种大学教材都直白地指出“零向量的方向不确定”“零向量与任一向量垂直”.但直到2012年,《中学数学杂志》2012年第1期的《与“零向量”有关的概念辨析及解题须知》与《数学通讯(下半月)》2012年第8期的《关于零向量的两个典型案例的思考与探究》两文都认为零向量的方向无法确定,不能说零向量与任一向量垂直.笔者亲历的对“零向量”这一概念的疑惑与争论持续了十年左右,笔者想说的是,阅读真的很重要,倘若我们放弃了阅读,可能数十年后的我们还在云遮雾绕中满眼迷茫. (二)在阅读中理顺知识由来,积累解题智慧 来看一道模考试题:
a·b=0”……蹊跷的是,既然向量有方向,为何从不提及零向量的方向?两个非零向量有夹角,那么零向量与任一向量的夹角如何定义?规定零向量与任一向量平行且数量积为0的合理性体现在哪?既然规定零向量与任一向量平行,那么能规定零向量与任一向量垂直吗?这样的疑惑不只是笔者有,笔者曾查阅十来年的期刊,其中的一些观点截然相反.直到笔者读到人教A版教材副主编章建跃博士刊发在《中小学数学(高中版)》2010年第9期上的《把精力集中在核心知识的研究上》一文: “在向量代数中,我们感兴趣的是向量的运算及其规律,而且首先是非零向量,因为它们有好的运算——加法,并由此延伸出数乘向量.为了使它的逆运算(即减法)完满、不留空白,必须引进零向量.这是零向量的核心意义,就像实数集中的0在运算中的地位一样.由于零向量的位置特殊,数学家们约定‘零向量的方向不确定’.这样,在处理问题时,可根据需要让零向量与某一向量平行或垂直.这是一种人为的、合乎习惯的并且方便于应用的规定……” 读到章建跃博士关于零向量方向的这份“终审判决”,笔者才算认清了事实的真相,而且章博士还精准地定位了零向量的核心价值,让笔者清楚地理解了教材编写的思路.在查阅资料中笔者还发现,苏教版教材对零向量的处理方式与大纲版教材和人教A版教材相同,而人教B版教材、北师大版教材、湘教版教材及多种大学教材都直白地指出“零向量的方向不确定”“零向量与任一向量垂直”.但直到2012年,《中学数学杂志》2012年第1期的《与“零向量”有关的概念辨析及解题须知》与《数学通讯(下半月)》2012年第8期的《关于零向量的两个典型案例的思考与探究》两文都认为零向量的方向无法确定,不能说零向量与任一向量垂直.笔者亲历的对“零向量”这一概念的疑惑与争论持续了十年左右,笔者想说的是,阅读真的很重要,倘若我们放弃了阅读,可能数十年后的我们还在云遮雾绕中满眼迷茫. (二)在阅读中理顺知识由来,积累解题智慧 来看一道模考试题: 
 这是以“Dandelin双球”模型为背景进行命制的一道数学文化试题,颇具新意.笔者的多位同事也在一起商讨此题的求解办法,令人意外的是,多位教学经验丰富的同事都不清楚本题的来源. 人教A版《数学》(选修2-1)教材第二章的引言部分中讲到,“用一垂直于圆锥的轴的平面截圆锥,截口曲线是一个圆……用一个不垂直于圆锥的轴的平面截圆锥,当截面与圆锥的轴夹角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线、双曲线.”如图2所示,2000多年前,阿波罗尼斯就是采用平面切割圆锥的方法来研究这几种曲线,“圆锥曲线”的名称由此而来.教材在“椭圆及其标准方程”部分的“探究与发现”栏目刊登了《为什么截口曲线是椭圆》一文,介绍了数学家Germinal Dandelin的方法:
这是以“Dandelin双球”模型为背景进行命制的一道数学文化试题,颇具新意.笔者的多位同事也在一起商讨此题的求解办法,令人意外的是,多位教学经验丰富的同事都不清楚本题的来源. 人教A版《数学》(选修2-1)教材第二章的引言部分中讲到,“用一垂直于圆锥的轴的平面截圆锥,截口曲线是一个圆……用一个不垂直于圆锥的轴的平面截圆锥,当截面与圆锥的轴夹角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线、双曲线.”如图2所示,2000多年前,阿波罗尼斯就是采用平面切割圆锥的方法来研究这几种曲线,“圆锥曲线”的名称由此而来.教材在“椭圆及其标准方程”部分的“探究与发现”栏目刊登了《为什么截口曲线是椭圆》一文,介绍了数学家Germinal Dandelin的方法: