外聘CEO职业经历、任期与公司经营战略变革的关系

      2020年江苏高考数学试卷坚持“立德树人，服务选才，引导教学”等核心立场，依旧是由易到难的命题规律，整体稳定，文理兼顾，紧扣大纲，结合教材，立足基础，适度创新.本套试卷在题型、题量、分值上与前两年相比保持不变，整体难度与上一年基本相当.试卷注重“三基”的考查，对基础知识、基本技能、基本思想方法的考查占了较大比重.试卷充分体现了“依纲扣本，引导教学，科学选拔”的命题理念，践行了“有利于促进学生健康发展，有利于科学地选拔人才，有利于维护社会公平”的三项原则，充分体现新课程标准的理念，值得品味.

      一、立足基础，突出主干

      试卷中的不少试题都是由课本教材中的例（习）题、练习题等进行适当的变式、改编、重组、嫁接等再加工而来的，是考生比较熟悉的，主要考查基础知识、基本技能、基本思想方法，如填空题中的第1～10题和解答题第15、16题等，都是源于课本改编而来的相对比较基础的题目，试题情境熟悉，朴实灵活，充分考查了学生的数学素质、思维品质与学习潜能，保证基本分值.

      例1 （2020年高考数学江苏卷第7题）已知f（x）是奇函数，当x≥0时，，则f（-8）的值是________.

      解析：由于yf（x）是奇函数，则.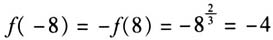

      故填答案：-4.

      点评：本题考查函数的奇偶性与解析式、函数值的求解，考查运算求解能力、数学运算等核心素养.函数作为高中数学的一条主线，串起高中数学的整个知识体系与架构，是高考中最基本的考点之一，作为基础性的知识，要加以熟练掌握与系统应用.

      试卷对支撑高中数学课程的主干知识进行重点考查，函数与导数（第7、12、17、19题）、数列（第11、20题）、平面解析几何（第6、14、18题）、立体几何（第9、15题）、三角函数与平面向量（第8、10、13、16题）等，占了总题量的75%，总分值的84%还多（数学Ⅰ卷），对《考试说明》（数学）中的8个C级考点进行了全面反复考查，基本覆盖了B级考点，适当兼顾了A级考点，考查全面，不偏不漏.

      二、强化思想，通性通法

      数学思想方法引领着数学的教学与学习，是数学的灵魂，试卷进一步强化数学思想方法的考查：（1）函数与方程思想，如第7、8、10、11、14、17、18、19题等都有所涉及；（2）分类与整合思想，如第5、11、13、14、17、19、20题等都有所涉及；（3）化归与转化思想，如第7、8、9、10、11、12、13、14、15、17、18、19、20题等都有所涉及；（4）特殊与一般思想，如第11、13、20题等都有所涉及；（5）统计与概率思想，如第3、4题等都有所涉及.这些数学思想方法穿插于不同试题之中，形成一个完整和谐的整体，充分考查考生的“三基”.

      试题淡化特殊性方面的技巧，突出试题最基本的通解通法的考查，没有特殊值验证、特殊模型应用等，有的只是最基本的数学方法，如第4题考查了列举法，第20题第（1）问涉及了反证法，第14、17、19、20题考查了构造法，而第12题中代数关系式的最值求解可以利用配凑法、消参法、待定系数法、判别式法、三角换元法及求导法等数学方法来处理与转化等.

      

      

      点评：破解此类问题都是有效联系条件中的代数关系式与结论中的代数关系式两者之间的关系，结合认真审视试题，合理巧妙变换，借助比较常见的通性通法来处理与解决，为不同层次的学生破解问题提供条件.

      三、凸显能力，突出创新

      试卷秉承重基础、重本质的一贯命题思路，在此有效凸显数学能力与数学核心素养，对学生的能力有较高的要求.特别是一些试题涉及多个知识点，具有一定的综合性，试题表述简练精准，知识点清晰不堆砌，解答题设问清楚有梯度，对不同基础、不同能力水平的学生都提供了适当的思考空间与能力要求，让不同能力水平的考生都有充分发挥的空间.例如第20题的数列新定义问题，第（1）问作为基础性问题，给60%的考生提供思考与破解的能力要求；第（2）问作为中等提高性问题，给20%的考生提供更进一步的分析能力、推理能力的拓展空间；第（3）问作为竞赛性问题，给5%的考生提供创造性解决问题的空间，合理梯度设置，确保试卷的区分度，有利于选拔不同层次的优秀人才.