中国企业战略管理四十年（1978-2018）：回顾、总结与展望

      “误中悟”就是在合适的情境下，从误区出发，激疑生惑，通过问题驱动，思维引擎，促进学生独立思考、分析探究、合作交流、讨论争辩，生成合理结论或有效方案或独到见解的过程.遵循“四个理解”设计“误中悟”课堂教学流程：问题情境—质疑审问—慎思参悟—明辨顿悟—误中笃行—反思悟道.“误中悟”教与学以理解学生为中心，以批判性思维为核心，突出问题解决的整体性学习和学习共同体的深度学习，强调批判性思考和自主学习.关键是激疑生惑，慎思参悟，追求顿悟、悟道，增强数学悟感，培养学生的创新精神和创新能力，培育数学学科核心素养.“误中悟”的基本主张是善待错误，把困惑变成反思，把反思变成收获，把错误变成资源.探寻“误之雾”的归因，探究“悟之固”的途径.

      函数是高中数学的重点内容，函数图象的描绘分析是学生的一项重要基本功.高中阶段介绍了很多基本初等函数，学生在掌握了这些基本初等函数的性质与图象以后，结合导数在函数单调性中的应用，在绘制陌生函数的图象时，会出现很多新的问题，如偏对称与对称、趋近与不趋近等.所绘制图象的准确度直接影响后续对函数问题的分析.图象绘制不准确，甚至会导致出现很多错误的判断.笔者以培养学生的函数图象作图能力为例，剖析在利用函数的单调性绘制函数的大致图象时容易疏忽的细节，引发一系列认识误区，引导学生去“雾”明“误”，纠“误”得“悟”，加强学生对作图细节的认识，促进学生学会以形带数、数形结合，培育直观想象核心素养，逐步学会“误中悟”的学习方式.

      一、课堂教学活动阶段1：学生的作图细节要点

      环节1：问题情境.

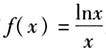      例1 作出函数的大致图象.

      问题1：作一个新的函数图象，需要做哪些准备工作呢？

      分析：函数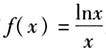的定义域为（0，+∞）.对函数f（x）求导，得，易得函数f（x）在区间（0，e]上单调递增，在区间[e，+∞）上单调递减.

      学生容易作出函数的大致图象，如图1所示.

      

      环节2：质疑审问.

      问题2：这个大致的函数图象是否准确呢？

      当x＞e时，f（x）＞0恒成立，不会出现负值，故这个大致函数图象不准确.

      环节3：慎思参悟.

      问题3：如何修改这个函数图象呢？你有没有接触过类似的函数？

      从熟悉到一般，借助指数函数的无限趋近特征来解决遇到的问题，如下页图2所示.结合函数的单调性，可得当x＞e时，f（x）单调递减，但是恒为正数.类比指数函数的图象，该函数在图象上的表现与x轴无限接近，但不相交.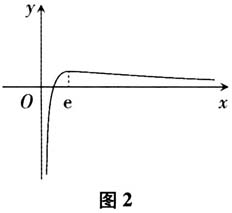

      

      环节4：明辨顿悟.

      从该例中可以得到作图细节的三个要点是：函数的定义域分析；函数的单调性分析；根据函数解析式的特征分析函数的整体数值变化趋势，类比初等函数（如指数函数）来理解和绘制函数图象的趋势.

      环节5：悟中笃行.

      

      

      问题4：这个函数图象是否有不恰当的地方呢？

      这里要处理的是定义域中的间断点1，类比反比例函数，如图4所示.

      

      当x从左侧趋近于1时，g（x）＜0，函数g（x）在（0，1）上单调递减，且趋近于-∞；当x从右侧趋近于1时，g（x）＞0，函数g（x）在（1，e]上单调递减，在[e，+∞）上单调递增，且趋近于+∞.

      环节6：反思悟道.