一、教材解析 向量是近代数学中的基础概念,向量理论具有深刻的数学内涵、丰富的物理背景,向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁[1].本节课是人教A版《数学4》(必修)第二章“平面向量”的起始课,内容包括“章引言”和“2.1平面向量的实际背景及基本概念”.“平面向量的实际背景及基本概念”这节课,从概念的形成角度看,重要的不是让学生知道向量的形式化定义及几个相关的概念,而是能让学生体会到获得数学研究对象、认识数学新对象的基本方法和基本思路,蕴含了用数学的观点刻画和研究事物的方法和途径. 本节课基本概念较多,但知识难度不大,为了帮助学生寻找一条清晰的主线,将琐碎的概念串起来,笔者将与数、形的相关概念的类比与联系作为突破口:类比数的概念(数的抽象过程、实数的绝对值及线段的长度)获得向量概念的定义及表示,类比数的集合(数的相等、0与1的特殊性)认识向量的集合,类比直线(段)的基本关系(平行或共线)认识向量的基本关系.让学生从中体会到认识一个数学概念的基本思路:从具体背景中抽象出共同特征一定义—表示—某些特殊对象或特殊关系. 二、教学目标 (1)了解向量的实际背景,理解平面向量的概念和向量的几何表示;掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量等概念;并会区分平行向量、相等向量和共线向量. (2)通过对向量的学习,使学生初步认识现实生活中的向量和数量的本质区别. (3)通过对学生关于向量与数量的识别能力的训练,培养学生认识客观事物的数学本质的能力. 三、教学重点、难点 教学重点:理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量. 教学难点:平行向量、相等向量和共线向量的区别和联系. 四、教学过程 (一)问题引入,让概念自然引入 问题1 如果你在教室门口,有人问你实验楼怎么走,你会如何回答? 设计意图:向量概念不是凭空产生的,它有着丰富的实际背景.通过对生活中常见问题的回答,引出关键词——方向和距离.而两者的结合让学生联想到位移,再联想到矢量,从矢量的定义引出既有大小又有方向的量,让学生感受到“既有大小又有方向的量”的客观存在,让学生体会引入平面向量概念的必要性,自然引出本节课的学习内容. (二)联系生活,让概念的形成自然 问题2 你能否再举出一些既有大小又有方向的量? 设计意图:在学生认知结构中存在大量既有大小又有方向的量,这样的追问,既可以调动学生学习的积极性,又可以在学生的举例中,观察到学生对概念属性的领悟,让学生形成对概念的初步认识,并积累丰富的典型实例,为进一步抽象概括做准备. 教师:在现实生活中就有相应的实例,如天气预报中的东南风3级.数学中,我们把既有大小又有方向的量进行抽象,就形成一种新的量,我们把它叫作向量[2](板书向量概念),这就是我们今天这堂课的主角.除了向量之外,还有相应的另一个量——只有大小没有方向的量,我们把它称之为数量. 追问:你能否再举出一些只有大小没有方向的量? 设计意图:数量是与向量相对的量,在学生的举例中,让学生充分感受生活中存在的不同属性的量,进一步加强学生对向量概念属性的认识,并为后面的类比奠定基础. (三)类比为桥,让概念的认识过程自然 问题3 数量如何来表示?能否从数量的表示方法中得到启发,找到向量的表示方法? 设计意图:该问题让学生在回忆数量表示的基础上,类比数量的表示方法,尝试得到向量的表示方法.在此过程中,让学生自己探求向量的表示方法,教师引导学生不断完善,形成两种向量的表示:几何表示和字母表示.并通过师生讨论得出结论:向量的一个属性是方向,我们用带有箭头的线段(有向线段)来表示,向量的另一个属性是大小,我们用|
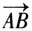
|表示向量
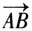
的长度(或称模),同样用|a|表示向量a的长度(或称模). 问题4 在实数集中,“0”是数的正负的分界点,“1”是“单位”,作用都很大.在向量的集合中,哪些是特殊的向量? 设计意图:用类比数集的方法初步认识向量的集合,引导学生学会面对一组新的数学对象时,首先应注意特殊对象.类比实数的学习,学生自然会想到两个特殊的向量:长度为0的向量(叫作零向量),长度为1的向量(叫作单位向量).教师归纳零向量和单位向量是从“大小”来看的特殊向量,并补充零向量和单位向量的表示方法,追问它们的方向属性. 问题5 如图1,设O是正六边形ABCDEF的中心,结合图中所示的向量,从“方向”上看,有哪些比较特殊的位置关系呢?(请学生到黑板板演)

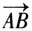 |表示向量
|表示向量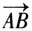 的长度(或称模),同样用|a|表示向量a的长度(或称模). 问题4 在实数集中,“0”是数的正负的分界点,“1”是“单位”,作用都很大.在向量的集合中,哪些是特殊的向量? 设计意图:用类比数集的方法初步认识向量的集合,引导学生学会面对一组新的数学对象时,首先应注意特殊对象.类比实数的学习,学生自然会想到两个特殊的向量:长度为0的向量(叫作零向量),长度为1的向量(叫作单位向量).教师归纳零向量和单位向量是从“大小”来看的特殊向量,并补充零向量和单位向量的表示方法,追问它们的方向属性. 问题5 如图1,设O是正六边形ABCDEF的中心,结合图中所示的向量,从“方向”上看,有哪些比较特殊的位置关系呢?(请学生到黑板板演)
的长度(或称模),同样用|a|表示向量a的长度(或称模). 问题4 在实数集中,“0”是数的正负的分界点,“1”是“单位”,作用都很大.在向量的集合中,哪些是特殊的向量? 设计意图:用类比数集的方法初步认识向量的集合,引导学生学会面对一组新的数学对象时,首先应注意特殊对象.类比实数的学习,学生自然会想到两个特殊的向量:长度为0的向量(叫作零向量),长度为1的向量(叫作单位向量).教师归纳零向量和单位向量是从“大小”来看的特殊向量,并补充零向量和单位向量的表示方法,追问它们的方向属性. 问题5 如图1,设O是正六边形ABCDEF的中心,结合图中所示的向量,从“方向”上看,有哪些比较特殊的位置关系呢?(请学生到黑板板演) 