一、问题的提出 2019年下半年,安徽省肥东县某校举办了青年教师岗位技能大赛,笔者有幸受邀担任数学学科评委,课题是人教A版《数学2》(必修)“平面与平面垂直的判定”.大部分教师基本功扎实,思路清晰、教学理念先进,较好地完成了教学任务.但遗憾的是,部分教师在教学中照本宣科,直接给出相关概念和定理,不能利用学生原有的认知结构引发学生思考,没有展现概念的生成过程.那么,如何优化本节课的教学呢?笔者进行了深入的分析与思考.现整理成文,以飨读者. 二、教学分析 (一)教材分析 教材对本节内容的要求是理解二面角定义及二面角的平面角,掌握面面垂直的判定定理及应用,在二面角及其平面角和面面垂直定理的建构过程中,体会类比、降维等数学思想. 二面角是一个全新的概念,它的度量需要教师类比异面直线所成角和直线与平面所成角的经验,用“平面化”的思想来定义.两个平面互相垂直是两个平面相交的特殊情况,在归纳面面垂直的判定定理时,引导学生类比面面平行的判定定理的生成过程,即把平面与平面的位置关系转化为直线与平面的位置关系,通过观察具体事例抽象概括判定定理. 基于以上分析,笔者认为本节课的教学目标为:(1)通过建构二面角及其平面角的过程,培养学生会用数学的思维思考问题;(2)通过面面垂直的判定定理的发现过程,培养学生会用数学的眼光观察问题;(3)通过给数学概念下定义,用符号语言表述判定定理,培养学生会用数学的语言表达问题;(4)体会化归、类比、降维等数学思想,培养学生发现问题和分析问题的能力. 教学重点:(1)二面角平面角的概念;(2)面面垂直的判定定理. 教学难点:二面角平面角概念的形成过程及面面垂直判定定理的运用. (二)学情分析 通过前面线面平行、面面平行、线面垂直等知识的学习,学生已经基本掌握了研究立体几何的一般方法——平面化,对线面、面面间关系的转化也有了初步认识.但本节内容对学生抽象概括能力、空间想象能力的要求较高,故采用启发引导、实践探究等多元结合的教学方法. 按照新课标的要求,本节课的设计遵循“类比归纳—动手操作—感知确认—思辨论证”的认识过程.教学中应从学生的“最近发展区”入手,引导学生归纳二面角的定义,探索二面角的度量,发现面面垂直的判定定理,帮助学生实现从具体到抽象、从感性到理性的过渡,从而完成概念的建构和定理的发现. 三、教学过程 (一)教学环节1:联系已学知识,类比生成定义 教师:前面我们学习了线面垂直的判定定理和两个平面平行的判定,请同学们回忆一下. 学生回答略. 教师:今天我们将研究两个相交平面的相关问题.在生产实践中,有许多情形涉及两个平面相交所成的角的问题,例如发射人造地球卫星时,卫星的轨道平面和地球赤道平面成一定的角度;修筑水坝时,水坝面和水平面成适当的角度;打开的门与门框所在的平面也成一定的角度;等等.为了解决实际问题,我们需要研究两个相交平面所成的角.今天我们来研究两个平面相交的特殊情况——平面与平面垂直的判定(多媒体展示视频和图片,板书课题). 设计意图:简单梳理已学知识,让学生感受到空间位置关系学习的“连贯性”、研究方法的“相似性”.列举丰富的生活实例,能增强课堂的趣味性,也为后面的探究活动埋下伏笔,使课堂探究活动有章可循、有据可依. 教师:同学们知道,一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫作射线.类似的,一条直线也可以把平面分成几个部分?每个部分可以叫作什么?(多媒体展示) 学生1:分为两个部分,每个部分叫作半平面. 教师:平面几何中“角”是怎样定义的? 学生2:从一点出发的两条射线所组成的图形叫作角(如图1). 教师:你能类比平面几何中角的定义给出二面角的定义吗? 学生3:从一条直线出发的两个半平面组成的空间图形称为二面角(如图2). 教师:仿照平面几何中角的记法∠AOB,二面角可以怎么表示?……
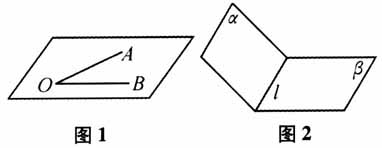
设计意图:重视过程教学就要开启学生原有的认知结构,为学生的思维展开提供空间.结合课件演示,启发学生类比“旧知”给半平面及二面角下定义,展示平面图形到空间图形的抽象过程、体验二面角图形的生成过程,激发学生的理性思维,协助学生循序渐进地构建二面角及其相关概念,使教学活动真正建立在学生自主活动的基础上,提升学生的直观想象和数学抽象的核心素养. (二)教学环节2:动手操作实验,主动探究新知 教师:角也可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.同样,二面角也可以看作是一个半平面以其棱为轴旋转而形成的图形.例如,我们常说“把门开大一些或小一些”,这说明二面角有大小.那么,如何去度量二面角的大小呢?请同学们回忆前面学习的异面直线所成角、直线和平面所成角,我们的度量方法是什么(教师带领学生回忆并总结)?
 设计意图:重视过程教学就要开启学生原有的认知结构,为学生的思维展开提供空间.结合课件演示,启发学生类比“旧知”给半平面及二面角下定义,展示平面图形到空间图形的抽象过程、体验二面角图形的生成过程,激发学生的理性思维,协助学生循序渐进地构建二面角及其相关概念,使教学活动真正建立在学生自主活动的基础上,提升学生的直观想象和数学抽象的核心素养. (二)教学环节2:动手操作实验,主动探究新知 教师:角也可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.同样,二面角也可以看作是一个半平面以其棱为轴旋转而形成的图形.例如,我们常说“把门开大一些或小一些”,这说明二面角有大小.那么,如何去度量二面角的大小呢?请同学们回忆前面学习的异面直线所成角、直线和平面所成角,我们的度量方法是什么(教师带领学生回忆并总结)?
设计意图:重视过程教学就要开启学生原有的认知结构,为学生的思维展开提供空间.结合课件演示,启发学生类比“旧知”给半平面及二面角下定义,展示平面图形到空间图形的抽象过程、体验二面角图形的生成过程,激发学生的理性思维,协助学生循序渐进地构建二面角及其相关概念,使教学活动真正建立在学生自主活动的基础上,提升学生的直观想象和数学抽象的核心素养. (二)教学环节2:动手操作实验,主动探究新知 教师:角也可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.同样,二面角也可以看作是一个半平面以其棱为轴旋转而形成的图形.例如,我们常说“把门开大一些或小一些”,这说明二面角有大小.那么,如何去度量二面角的大小呢?请同学们回忆前面学习的异面直线所成角、直线和平面所成角,我们的度量方法是什么(教师带领学生回忆并总结)?