层次分析法在质量管理统计方法中的应用

      本文将层次分析法运用于传统的质量管理方法——因果分析图中，并编制了计算机程序，通用性强。

      层次分析法(The Analytic Hierarchy Process)是美国匹兹堡大学教授T·L·Saaty提出的一种系统分析方法。它把一个复杂问题中的各种因素划分为相互联系的有序层次并使之条理化。传统的质量管理统计方法——因果分析图运用层次分析理论，通过建立递阶层次结构和进行数学计算，用权值大小清楚反映了主次因素，突出了问题的关键，弥补了传统方法缺乏定量分析的不足，把定性分析与定量分析有机地结合起来，促进了因果分析法的推广，使权值因果分析图具有广阔的应用价值。本文以西北合成药厂在开展采用国际标准提高巴比妥一次优级品率活动中绘制的“重乙基酯比重高”因果分析图（图1）为例，说明层次分析法的应用。

      

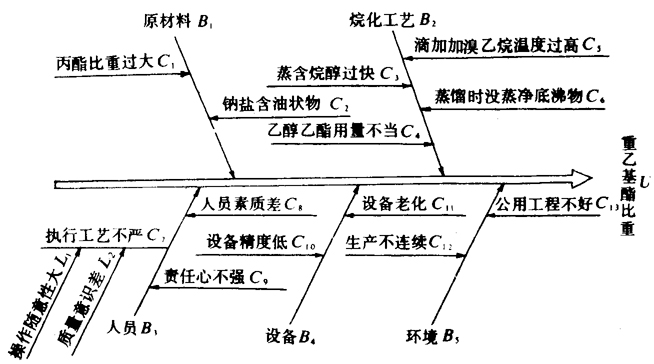      图1 重乙基酯比重高因果分析图

      1.建立递阶层次结构模型

      这一步将问题所包含的因素按属性不同，划分为最高层，中间层和最低层。最高层只有一个元素，是影响质量问题的结果；中间层是影响质量问题的大原因、中原因；最低层是影响质量问题的小原因或更细小的原因。例题建立的层次结构模型见图2。

      

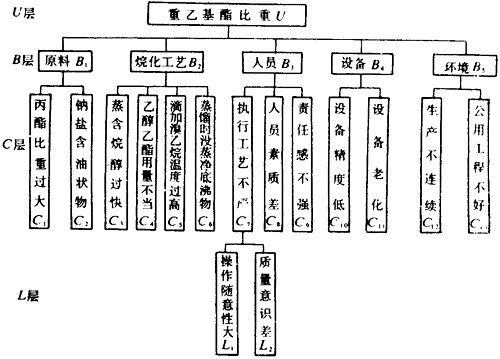      图2 层次模型

      2.构造两两比较判断矩阵

      这一步要仔细反复考虑两个相比较的元素，哪个更重要，重要多少，并对重要程度赋予一定权值。这里打分采用1～9的比例标度（见表1）。这一步对定量分析的结果满意与否至关重要。对于n个元素来说，两两比较判断矩阵为

      

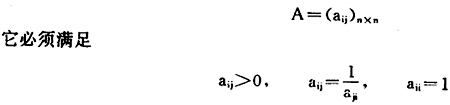      表1 标度的含义

      标度标度含义

      1

      表示两个元素相比，具有同样重要性

      3

      表示两个元素相比，一个元素比另一个元素稍微重要

      5

      表示两个元素相比，一个元素比另一个元素明显重要

      7

      表示两个元素相比，一个元素比另一个元素强烈重要

      9

      表示两个元素相比，一个元素比另一个元素极端重要

      （2,4,6,8为上述相邻判断的中值）

      在举例中，按照各类因素间的隶属关系把它们分为四个层次，对问题建立的层次结构模型各因素的重要性关系构造判断矩阵（见表2、3、4、5、6、7、8）。

      

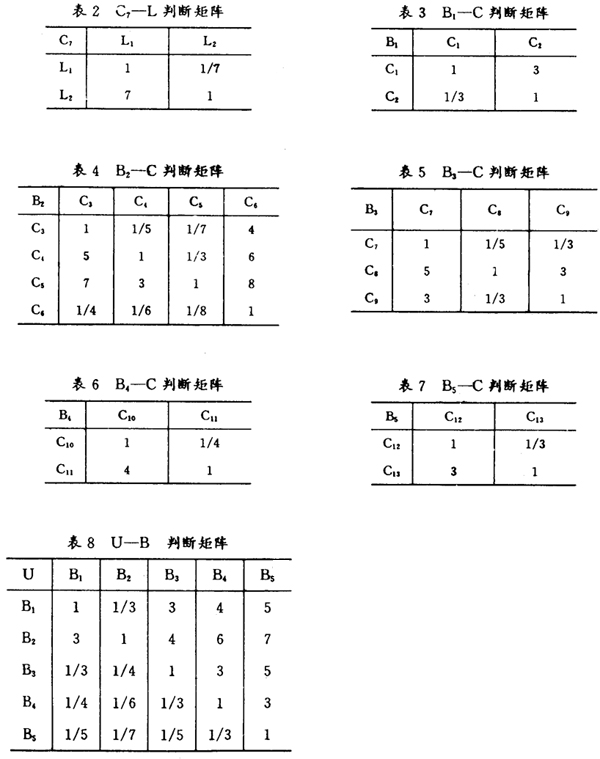      3.层次单排序及一致性检验

      (1)层次单排序

      先解出判断矩阵A的最大特征值λ[,max]再利用

      Aω＝λ[,max]ω

      解出λ[,max]所对应的特征向量ω，ω经过标准化后，即为同一层次中相应元素对于上一层次中某个因素相对重要性的排序权值。

      层次分析法计算的根本问题是如何计算矩阵最大特征根λ[,max]及其对应的特征向量ω，下面介绍用方根法求算λ[,max]和ω。

      第一步 计算判断矩阵每一行元素乘积。

      

      

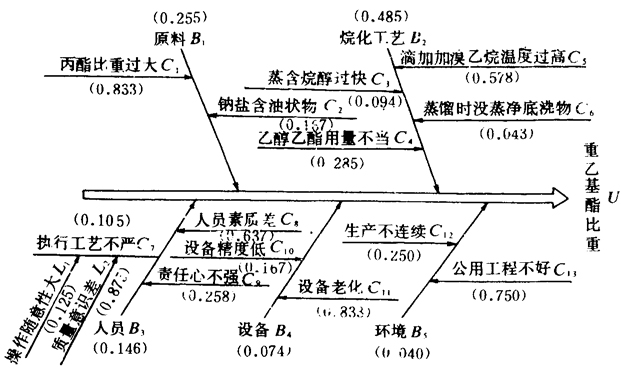      图3 权值因果分析图

      (2)一致性检验

      由于问题复杂程度不尽相同，不可能要求所有判断都完全一致，但却应该使判断有大体上的一致性。因此，需要对判断矩阵A进行一致性检验。首先计算A的一致性指标C.I

      

      式中，n为判断矩阵的阶数。当A具有完全一致性时，C.I＝0。λ[,max]-n愈大，C.I愈大，矩阵的一致性愈差。当判断A是否具有满意的一致性，还需将C.I与平均随机一致性指数R.I进行比较。对于1～9阶判断矩阵，T.L.Saaty给出了R.I值（见表9）。

      表9 随机性指标R.I值

      阶数n 1 23 4 5 6 7 8 9

       R.I 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45

      当时，就认为判断矩阵A具有满意的一致性，否则要对A重新调整，直到具有满意的一致性为止。