民族国家的“错觉”：差异与认同

      在《徐利治谈治学方法和数学教育》一书中，徐教授指出“数学是模式的科学”.罗增儒教授在《数学解题引论》中也将模式识别作为第一个解题策略介绍给读者.的确，无论是数学中的概念和命题，或是问题和方法，都应被看成一种具有普遍意义的模式，“模式”的概念能更为深刻地揭示数学的本质.如在解题中常常需依据导数法则构造辅助函数，解决以抽象导函数为背景的函数性质、函数不等式或比较大小的问题，但导数运算法则这个模型往往又被命题者用各种手法掩盖起来，这就需要解题者以“法则”模型为基准，以不变应万变.由于数学问题的形式千姿百态，因此需要我们不断地归纳总结变化规律，提高解题技能.本文尝试对此类问题的演化规律做些归纳，希望对读者有所帮助.

      容易发现，条件中含有f（x）的抽象函数问题，常见的有三类：

      

      此类问题特别在2015年高考全国Ⅱ卷和福建卷同时出现后，就在各种考试中频频现身，迫使命题者对其不断演化创新.

      一、改变条件或目标式子的结构

      将条件不等式或所解不等式的结构进行变形是命题者比较惯用的手法，所以要提高我们的洞察力和数学运算的化归能力，防止一叶障目不见泰山.

      

      评注 本题目标是解不等式，但函数f（x-3）未知，因此解题关键是构造辅助函数，利用函数单调性和导数之间的关系判断出函数的单调性，然后将所求不等式转化为对应函数值的关系，根据单调性定义将原抽象函数不等式转化为关于x的具体不等式求解.题目将条件和目标不等式结构进行了一定程度的变形，提高了运算素养考查力度.

      

      二、升级抽象函数或已知函数

      

      评注 构造函数的基本策略就是从已知条件或问题目标中发掘信息.本题从条件视角观察，给出的应是某函数导数不等式，因此将条件不等式移项右边化为0，再通过常数1的导数为0及左边式子的结构，归结为关于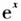商的导数；从结论视角，结合条件信息将目标不等式化为某函数的两函数值间的大小关系，从而显现出需构造的函数.

      

      三、变直接为间接——放缩条件不等式

      有些问题依据条件并不能直接构造出导数大于0（或小于0）的不等式，而是要通过适当的放缩才能获得所需要的不等式.解这类不等式的关键点也是难点仍然是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②根据目标不等式的结构特征的共性归纳构造恰当的函数.

      

      评注 解此类题切莫将整个条件不等式作为构造函数的对象，应注意分解与重组，考虑其局部特征再联系目标不等式的相关信息来构造辅助函数.

      

      四、变条件不等式为等式——研究抽象函数的性质

      将条件含有抽象函数导数的不等式变为等式，表面上看似乎变得简单了，事实上并非如此，但联系已知条件和结论，准确构造出符合题意的辅助函数仍然是解题的关键！进而利用辅助函数与原抽象函数的关系，求导研究抽象函数的单调性、极值和最值等性质.

      

      所以f（x）在（0，+∞）上为减函数.故选B.

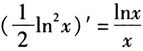      评注 本例通过条件等式构造函数，由于新函数的导数已知，因此以新函数为桥梁表示出函数f（x），进而利用二次求导探求f（x）的单调性；当然也可以利用已知的导函数找原函数，化抽象为具体，如本题通过，可知.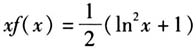

      变式4 设定义在（0，+∞）上的函数f（x）满足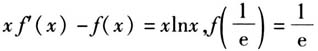，则f（x）（

       ）.