思想政治教育内化过程中的情感意蕴

      一、发现问题

      波利亚在《怎样解题》中给出了宏观的解题程序并把它们总结在了“怎样解题表”中，即把解题过程鲜明地分为四步：弄清问题、拟定计划、实现计划、回顾.波利亚的总结很准确而且很实用，被广大教师运用到了日常教学中.但是这样高度精练的宏观方法对中学生来说仍然很抽象.

      现在的数学学习中出现了一种很奇怪的现象：有一部分学生上课也认真听讲，认真做笔记，下课也认真复习，但是却考不好.很多老师把这一类学生总结为“不会学”，但笔者认为这部分学生并不是不会学，而是“不会想”.“不会想”是指学生不会思考，这并不是说学生智商不够高，而是没有正确的思考方法.如果我们把一次数学考试看做是打一场硬仗，那么要想赢得胜利我们就要具备两个东西——装备和策略.“装备”指的是基础知识储备，这取决于学生平时的学习态度.“策略”就是思考模式，一个高效的思考模式不仅可以很快找到思路，并且可以顺利地找到解题计划.

      学生在解决数学题时，一般的思考模式都是：读题→弄清楚题干给了哪些条件→分析这些条件和问题之间的联系-→拟定出解题计划.笔者把这种思考模式称为正向思考模式，这种思考模式就好像是从起点瞭望终点来分析解题路径.那么本文笔者提出一种逆向思考模式，即从终点回望起点.先从问题入手，通过先假定问题已经被解决来分析到底需要哪些条件.希望读者在读完此文后能有所收获，在日后解决数学问题的过程中，能有目的地一步一步地找到答案.

      二、逆向思考方式的步骤

      逆向思维方式的基本步骤分为五步，分别为：

      （1）读题，着眼于问题，以此作为自己的“目标”.

      （2）厘清“目标”到底长什么样子，即可假定如果“目标”成立则意味着什么.再运用已有的基础知识将目标转化成新目标.

      （3）逐步缩小“新目标”的范围，缩小范围的方法一般是化简或者等价转换，得到“终极目标”.

      （4）观察转化完的“终极目标”的特点，结合题设条件求证.

      （5）在草稿纸上把（4）→（3）→（2）→（1）写出来，即为解题方法.

      三、逆向思考方式的例题研究

      我们先以一道椭圆的高考题为例：

      例1 （2018年全国卷I19）设椭圆的右焦点为F，过F的直线l与C交于A、B两点，点M的坐标为（2，0）.

      （Ⅱ）设O为坐标原点，证明∠OMA=∠OMB.我们先把草图画出来，如图1所示.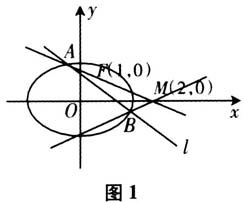

      

      第二问的程序性思考方式步骤如下：

      （1）读题，着眼于问题，以此作为自己的“目标”.例如这道题是让证明∠OMA=∠OMB.

      

      （4）观察转化完的“终极目标”的特点，结合题设条件求解.例如我们观察上面这个式子就会发现我们需要把直线AB的方程与椭圆的方程联立，再用韦达定理得到.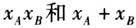

      （5）在草稿纸上把（4）→（3）→（2）→（1）写出来，即为解题方法.

      很多学生在做这道题时，由于定势思维，知道要把直线AB的方程与椭圆的方程联立，进而通过韦达定理得到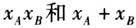.但是这样思考下来，下一步何去何从就不得而知了，这两个式子到底要用在什么地方？到底要证明什么？于是就陷入了一个黑洞越来越混乱.但是如果逆向考虑，那么每一步的目的性都很强，就不会存在没有思路的情况了.

      下面我们再用这种方法来分析一道抛物线的高考题，如下：

      例2 （2018年全国卷Ⅱ19）设抛物线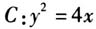的焦点为F，过F且斜率为k的直线l与C交于A、B两点，AB=8.

      （Ⅱ）求过点A、B且与抛物线C的准线相切的圆的方程.

      首先我们把图象画出来，如图2所示.

      

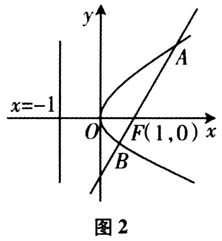      第二问的程序性思考步骤为：

      （1）读题，着眼于问题，以此作为自己的“目标”.例如这道题是让求圆的方程.

      （2）弄清楚“目标”到底长什么样子，即假定如果“目标”成立则意味着什么，再运用已有的基础知识将目标进行转化.例如这道题的问题是求“圆的方程”，圆的一般方程是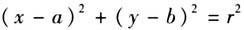的形式，那么“新目标”就是要求出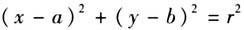中的圆心（a，b）和r.