数字化转型对企业员工薪酬的影响研究

      近年来，随着HPM视角下课例研究的深入开展以及一系列相关课例的发表，越来越多的数学教师开始关注HPM的教学理念、教育价值和教学策略.一般说来，数学教学中运用数学史料的方式有附加式、复制式、顺应式和重构式.除了附加式（介绍数学家的生平轶事、提供数学史阅读材料等）外，其他三种方式都与问题提出息息相关：复制式指的原始材料的直接采用（有时需要进行必要的语言转换），其中最主要的材料之一就是历史上的数学问题；顺应式指的是对数学史料的改编，包括对问题的改编；重构式是指借助一系列由易至难、环环相扣的问题串，再现知识的发生和发展过程，因此，在HPM视角下的数学教学中，数学问题乃是数学史的最重要的载体.

      另一方面，近年来，高考数学卷中相继出现了一些涉及数学文化的问题，这些问题引起人们的浓厚兴趣，已有大量文献对这些问题做过分析.数学史是数学文化的重要组成部分，讨论高考数学文化题，都绕不开基于数学史的问题.尽管已有部分文献对数学文化或数学史问题进行了分类，但分类方法还有待于进一步论证、细化和修正.本文的研究问题是：如何从数学史料出发，编制数学问题？高考数学卷中涉及数学史的问题反映了问题提出的哪些策略？

      我们希望在已有相关研究的基础上，建立“基于数学史的问题提出策略”的分类框架，并用于部分高考试题以及高中数学典型问题的分析，为未来HPM视角下的课堂教学和试题命制提供参考.

      二、基于数学史料的问题提出策略

      美国学者希尔佛（Silver）等人的研究表明，根据已知情境或已知问题提出新问题的具体策略有四种：

      ·条件式策略，即改变给定情境的条件而保持其目标不变，提出新问题；

      ·目标式策略，即改变给定情境的目标而保持其条件不变，提出新问题；

      ·对称式策略，即将给定情境中的条件和目标互换，提出新问题；

      ·链接式策略，即以给定情境的目标作为已知条件，提出新问题.

      其中前两种策略即为所谓的“否定属性”（what-if-not）策略.如果给定情境是含有条件和目标（或结论）的数学史材料（主要是数学命题和数学问题），那么相应地，“基于数学史料的问题提出策略”也包含上述四类，从数学史运用方式上说，这四种策略都属于顺应式.但是，希尔佛在其研究中所发现的问题提出策略，并不考虑课堂教学的需求，而本文所说的“基于数学史的问题提出策略”是服务于课堂教学的，因而有其特殊性.对于含有条件和目标（或结论）的数学史料来说，具体体现在以下几个方面：

      ·当数学史料完全满足课堂教学需求，即满足科学性、有效性、可学性、趣味性和人文性时，无需对其进行改编，因此，基于数学史料的问题提出策略应该包含“复制式策略”，即除语言翻译外，对情境、条件、目标（或结论）不加改编而直接采用.

      ·当数学史料部分满足课堂教学需求，但未能体现可学性、趣味性或人文性时，需要补充情境或对原有情境进行改编，但不改变史料中的条件和目标（或结论），这种策略称为“情境式策略”.

      ·针对一则数学史料，采用以上各类策略所提出的问题，都无法满足课堂教学需求，此时，教师需要同时改变史料中的情境、条件和目标（或结论），此时的策略称为“自由式策略”.

      对于不含条件或目标（或结论）的数学史料（主要是指概念定义、作图工具等），为了编制满足课堂教学需求的问题，需要设定条件或目标，此时的策略也属于“自由式策略”.

      因此，“基于数学史料的问题提出策略”至少有七类，见表1.

      

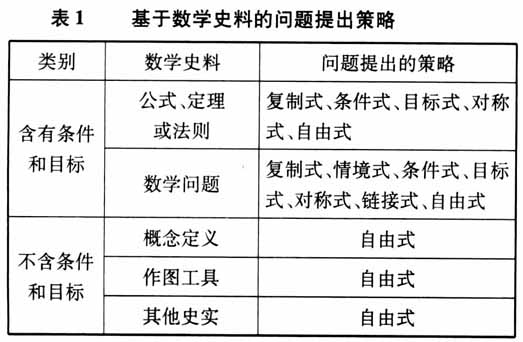      例如，《九章算术》勾股章中设有如下问题（通常称为“勾股容方问题”）：“今有勾五步，股十二步，问：勾中容方几何？”如果我们以该问题作为出发点，运用各种策略，分别可以提出以下新问题.

      问题1：已知直角三角形的两条直角边的长分别为5和12，求与该直角三角形具有公共直角的内接正方形的边长.（复制式）

      问题2：有一块直角三角形空地，直角边长分别为5米和12米.现要在该空地上建一个面积最大的正方形花坛，求该花坛的边长.（情境式）

      问题3：已知直角三角形的两条直角边长分别为7米和25米，求与直角三角形具有公共直角的内接正方形的边长.（条件式）

      问题4：已知直角三角形的直角边为a和b，求其内接正方形的边长.（条件式）

      问题5：若直角三角形两条直角边分别为a和b，则内接正方形边长为.你觉得古人是如何得到这个结果的？（条件式）

      问题6：已知直角三角形的直角边为5和12，求其内接正方形的面积.（目标式）

      问题7：已知直角三角形内接正方形（与直角三角形有公共直角）的边长为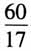，斜边为13，求直角边.（对称式）