企业并购依赖的缘由和后果：基于知识基础理论和成长压力理论的研究

      一、问题的提出

      随着新课程改革的不断深入，《普通高中数学课程标准（2017年版）》提出的“四基四能”与“数学核心素养”得到学者的高度关注，成为研究的热点.新课标倡导，教学应以生为本，注重师生互动，给学生创造良好的学习氛围等.这些要点也与生态课堂中多样性、交互性、整体性的特点相吻合，这表明生态课堂的构建对落实核心素养具有积极作用.“课堂生态学”的概念最先是由美国教育学家沃勒在1932年提出.近几年，国内研究生态课堂的视角也已逐渐从理念层面转向实际操作层面.

      万文涛教授在生态课堂的研究中提出了“学思行省”四个教学环节，能够帮助学生发展自身素养.教学中为了更好地设计“学思行省”教学环节，笔者在阅读文献的基础上对“学思行省”进行了细分，分别为“三学、三思、三行、三省”.具体如图1所示：

      

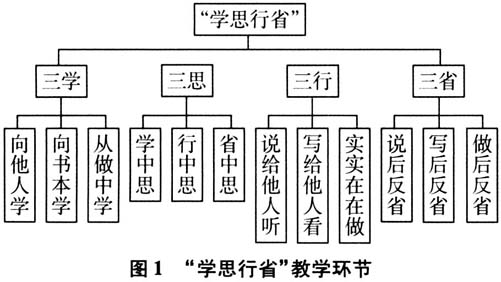
      二、基于“学思行省”的教学设计举隅

      函数作为高中数学的重要内容，一是因为函数思想的价值；二是因为函数的应用价值.本文以北师大版数学必修1第四章“函数应用”中“利用函数性质判定方程解的存在”为例，谈谈利用“学思行省”来进行高中数学教学设计.

      （一）教学目标

      （1）结合学过的函数图象，了解函数零点与方程解的关系.

      （2）结合具体连续函数及其图象的特点，了解函数零点存在定理.

      （3）在方程与函数的转换中，体会数形结合的思想，类比转化的思想.

      （二）教学重点

      （1）了解函数零点、方程的解、函数图象与x轴交点的横坐标之间的关系.

      （2）掌握零点存在定理并熟练运用.

      （三）教学难点

      探究零点存在的条件，并能利用零点存在定理解题.

      （四）教学过程

      1.旧知引入，思维碰撞

      问题1：方程是否有实数解？

      预设：解方程可得x=-2，x=3.

      问题2：可否利用函数与方程的联系解题？

      预设：设，画出f（x）的图象，找出f（x）图象与x轴交点的横坐标.

      问题3：方程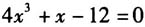是否有实数解？

      预设：学生不会很快得出答案.

      设计意图：孔子曾言：“疑是思之始，学之端.”在短短的引入之中，也包含着一次小的“学思行省”循环，温故解方程即是“学”，在解决方程中进行了“思”，“思”后说给他人听为“行”，说后反“省”类比解决问题3却发现解决不了.学生在这一过程中，由于问题难度的加深，产生了对于知识探求的兴趣，为下一轮“学思行省”循环做好心理铺垫.在这一过程中也培养了学生分析问题、解决问题的能力.

      2.交流梳理，初得零点

      用PPT展示出零点的定义：我们把函数y=f（x）的图象与x轴的交点的横坐标称为这个函数的零点.

      问题4：函数的零点是一个点吗？

      预设：它是点的横坐标，是一个实数.

      问题5：函数y=f（x）的零点与方程f（x）=0的解是什么关系？

      预设：两者是等价的关系.

      问题6：还有没有与之存在等价关系的？

      预设：函数y=f（x）的图象与x轴交点的横坐标.（展示图2）

      

      设计意图：这一环节同样是一个完整的“学思行省”过程，学生“学”到零点的定义，“思”零点是否是一个点，通过定义知道不是点，是横坐标，接着“行”，将心中所思说给他人听，最后教师引导学生“省”，思考函数图象函数的零点与方程的解有什么联系，让学生感悟到三者之间的等价关系，得出可以利用函数的性质来判定方程是否有解，也为下一个循环做好铺垫.

      3.抽象探究，判定零点

      通过海豚跳跃图（图3）判断海豚从A点到B点是否穿过了海平面，从A点到C点是否穿过海平面.在学生对比得到答案之后，展示动画的海豚跳跃画面，引导学生抽象成函数的图象，让学生进行思考.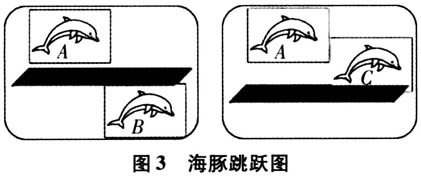

      

      问题7：如何判定函数y=f（x）在区间[a，b]内存在零点？根据学案，进行思考.