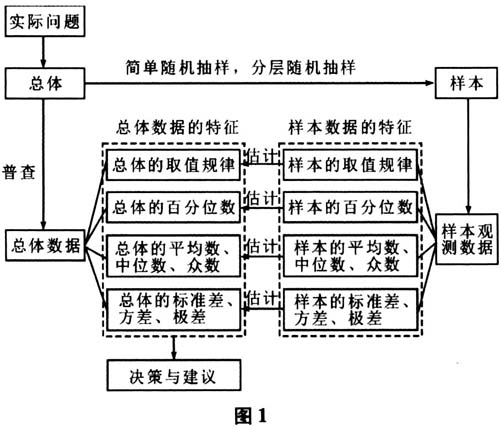
统计学有多种不同的定义,综合来说,统计学是收集、处理、分析、解释数据并从数据中得出结论的科学.作为专门研究有效收集和分析数据的科学,“可以说,凡是一个涉及数据处理的实际问题,都应该利用统计学方法去分析它、解决它”[1].统计方法不仅有用,而且对于理解周围的世界经常也是不可或缺的,它提供了对许多现象获得新见解的方法.现在统计学已深入科学、技术、工程和现代社会生活的各个方面.尤其是当我们进入了大数据时代和“互联网+”时代,作为研究数据分析的重要数学技术,统计学方法在相关领域的应用已成为“数学应用的主要方法”[2]. 从新中国成立以来,在中学数学课程中,统计经历从无到有、从描述统计到推断统计、从选修变为必修的过程,其要求和地位都在不断提高.《普通高中数学课程标准(2017年版)》(以下简称《课标(2017年版)》)把“概率与统计”与“函数”“代数与几何”并列作为高中数学课程内容主线,贯穿整个高中数学课程.高中统计除在初中统计基础上进一步学习数据收集和整理的方法、数据直观图表的表示方法、数据统计特征的刻画方法外,要求能用样本的统计特征推断总体的统计特征,包括单变量总体集中趋势参数、离散程度参数、取值规律和百分位数的估计,双变量总体的相关关系、一元线性回归模型和独立性的推断.相比初中统计以描述统计为主,高中统计以推断统计为主,更加强调数据的随机性. 在统计的学习过程中,应让学生感悟在实际生活中进行科学决策的必要性和可行性;体会统计思维与确定性思维的差异、归纳推断与演绎证明的差异;通过实际操作、计算机模拟等活动,积累数据分析的经验.通过统计的学习,还应帮助学生建立正确的随机观念,养成通过数据来分析问题的习惯,学会抓住事物的主要因素等,发展数据分析、数学建模、逻辑推理、数学运算和数学抽象等数学学科核心素养,实现统计的教育价值. 一、本章内容及学习要求 按照《课标(2017年版)》的要求,必修课程“统计”的主要内容包括:获取数据的基本途径及相关概念、抽样、统计图表、用样本估计总体.具体要求如下: (一)获取数据的基本途径及相关概念 (1)知道获取数据的基本途径,包括:统计报表和年鉴、社会调查、试验设计、普查和抽样、互联网等. (2)了解总体、样本、样本量的概念,了解数据的随机性. (二)抽样 (1)简单随机抽样. 通过实例,了解简单随机抽样的含义及其解决问题的过程,掌握两种简单随机抽样方法:抽签法和随机数法.会计算样本均值和样本方差,了解样本与总体的关系. (2)分层随机抽样. 通过实例,了解分层随机抽样的特点和适用范围,了解分层随机抽样的必要性,掌握各层样本量比例分配的方法.结合具体实例,掌握分层随机抽样的样本均值和样本方差. (3)抽样方法的选择. 在简单的实际情境中,能根据实际问题的特点,设计恰当的抽样方法解决问题. (三)统计图表 能根据实际问题的特点,选择恰当的统计图表对数据进行可视化描述,体会合理使用统计图表的重要性. (四)用样本估计总体 (1)结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数),理解集中趋势参数的统计含义. (2)结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义. (3)结合实例,能用样本估计总体的取值规律. (4)结合实例,能用样本估计百分位数,理解百分位数的统计含义. 二、本章知识结构
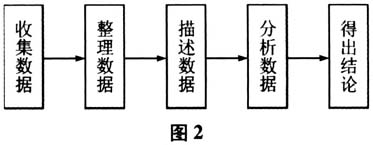
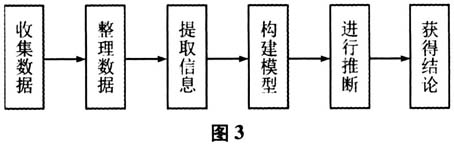
三、突出数据分析的基本过程,在过程中学习数据分析方法 统计是通过数据分析来解决问题的,数据分析的过程体现了统计解决问题的基本思路.因此,让学生了解这个过程,对整体把握统计学科的特点,理解具体的数据分析方法和应用数据分析方法解决实际问题都是非常重要的.数据分析的过程存在多种不同的划分方法,如图2和图3所示,其中图3是《课标(2017年版)》的划分方法.虽然不同划分方法中的环节数、每个环节提法等不完全一致,但都遵循从收集数据到分析数据再到得出结论的基本过程.
本章内容主要根据数据分析的基本过程进行安排,把学习内容分为三节,“9.1随机抽样”主要学习收集和整理数据的方法,“9.2样本估计总体”主要学习分析数据的方法,包括数据直观图表的表示方法和数据统计特征的刻画方法等,以及根据样本数据的统计特征估计总体的统计特征,“9.3统计案例公司员工的肥胖情况调查分析”是对前两节所学知识的综合应用.
 三、突出数据分析的基本过程,在过程中学习数据分析方法 统计是通过数据分析来解决问题的,数据分析的过程体现了统计解决问题的基本思路.因此,让学生了解这个过程,对整体把握统计学科的特点,理解具体的数据分析方法和应用数据分析方法解决实际问题都是非常重要的.数据分析的过程存在多种不同的划分方法,如图2和图3所示,其中图3是《课标(2017年版)》的划分方法.虽然不同划分方法中的环节数、每个环节提法等不完全一致,但都遵循从收集数据到分析数据再到得出结论的基本过程.
三、突出数据分析的基本过程,在过程中学习数据分析方法 统计是通过数据分析来解决问题的,数据分析的过程体现了统计解决问题的基本思路.因此,让学生了解这个过程,对整体把握统计学科的特点,理解具体的数据分析方法和应用数据分析方法解决实际问题都是非常重要的.数据分析的过程存在多种不同的划分方法,如图2和图3所示,其中图3是《课标(2017年版)》的划分方法.虽然不同划分方法中的环节数、每个环节提法等不完全一致,但都遵循从收集数据到分析数据再到得出结论的基本过程. 
 本章内容主要根据数据分析的基本过程进行安排,把学习内容分为三节,“9.1随机抽样”主要学习收集和整理数据的方法,“9.2样本估计总体”主要学习分析数据的方法,包括数据直观图表的表示方法和数据统计特征的刻画方法等,以及根据样本数据的统计特征估计总体的统计特征,“9.3统计案例公司员工的肥胖情况调查分析”是对前两节所学知识的综合应用.
本章内容主要根据数据分析的基本过程进行安排,把学习内容分为三节,“9.1随机抽样”主要学习收集和整理数据的方法,“9.2样本估计总体”主要学习分析数据的方法,包括数据直观图表的表示方法和数据统计特征的刻画方法等,以及根据样本数据的统计特征估计总体的统计特征,“9.3统计案例公司员工的肥胖情况调查分析”是对前两节所学知识的综合应用.