武汉大学机构用户,欢迎您!
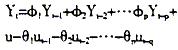 式中
式中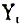 代表国民生产总值,
代表国民生产总值,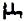 是随机误差,则称该模型为(p,q)阶自回归移动平均模型,记为ARMA(p,q)。随机项
是随机误差,则称该模型为(p,q)阶自回归移动平均模型,记为ARMA(p,q)。随机项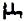 服从均值为0,方差为
服从均值为0,方差为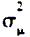 的正态分布,是白噪声序列。当模型中的
的正态分布,是白噪声序列。当模型中的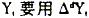 (差分算子)来代替时,则称该模型为单整自回归移动平均模型,记为ARIMA(p,d,q)。如果经济变量自身是平豫的,可以直接建立ARMA模型,则可以认为在短期内,各种冲击有可能对经济运行产生明显的震荡,但从长期的观点来看,经济运行本身可以依赖自身的力量去调整恢复,这种建模方式反映了凯恩斯主义的观点。相反,如果ARIMA模型同事实更为吻合的话,说明外部冲击可能对经济运行造成持久的影响,经济运行很难自行调节回到受冲击之前的状态,这恰恰反映了RBC理论的观点。如果我们依据RBC观点建立的模型能够通过检验,那么就可以从一个侧面间接证明RBC理论。 三、数据的选取与模型的验证 对中国近代经济史研究最大的困难在于原始数据的缺乏,既缺乏国民生产总值的连续数字,也没有各部门产值、产量等指标的完整数据。本文采用中国进口贸易额作为替代变量,以此分析整个经济波动的情况。这是因为:第一,在当时所有的统计数字中,由海关统计的进出口贸易额时间序列最长,可信度最高;第二,一个国家的进出口额变动是同该国经济状况密切相关的。国内经济增长时,对进口消费品和生产资料的需求会相应增加,而当国内经济不景气时,对进口品的需求也会相应减少。 表1 附图
(差分算子)来代替时,则称该模型为单整自回归移动平均模型,记为ARIMA(p,d,q)。如果经济变量自身是平豫的,可以直接建立ARMA模型,则可以认为在短期内,各种冲击有可能对经济运行产生明显的震荡,但从长期的观点来看,经济运行本身可以依赖自身的力量去调整恢复,这种建模方式反映了凯恩斯主义的观点。相反,如果ARIMA模型同事实更为吻合的话,说明外部冲击可能对经济运行造成持久的影响,经济运行很难自行调节回到受冲击之前的状态,这恰恰反映了RBC理论的观点。如果我们依据RBC观点建立的模型能够通过检验,那么就可以从一个侧面间接证明RBC理论。 三、数据的选取与模型的验证 对中国近代经济史研究最大的困难在于原始数据的缺乏,既缺乏国民生产总值的连续数字,也没有各部门产值、产量等指标的完整数据。本文采用中国进口贸易额作为替代变量,以此分析整个经济波动的情况。这是因为:第一,在当时所有的统计数字中,由海关统计的进出口贸易额时间序列最长,可信度最高;第二,一个国家的进出口额变动是同该国经济状况密切相关的。国内经济增长时,对进口消费品和生产资料的需求会相应增加,而当国内经济不景气时,对进口品的需求也会相应减少。 表1 附图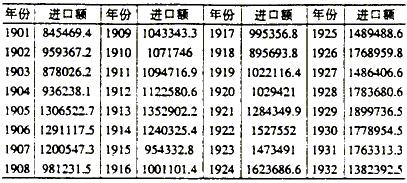 (数据来源:转引《中国近代经济发展史》,刘佛丁,1999) 1901-1932年间海关统计的进口贸易额,数据按1936年不变价格做了调整,见表1。 数据分析使用Eviews3.1。 对进口额(以im表示)数据做折线图: 附图
(数据来源:转引《中国近代经济发展史》,刘佛丁,1999) 1901-1932年间海关统计的进口贸易额,数据按1936年不变价格做了调整,见表1。 数据分析使用Eviews3.1。 对进口额(以im表示)数据做折线图: 附图 图1 由图1可见,在1920年代以后,im序列存在明显的上升趋势。数据不平稳,ARMA模型可能不适用。 为谨慎起见对im做单位根检验(c,0,0): 表2 ADF Test Statistic -0.732387 1% Critical Value* -3.6852 5% Critical Value -2.9705 10% Critical Value -2.6242 可见,im在10%的显著性水平下也不能通过检验,序列存在单位根。 对数据做一阶差分,令dim=im-im(-1),对dim做折线图: 附图
图1 由图1可见,在1920年代以后,im序列存在明显的上升趋势。数据不平稳,ARMA模型可能不适用。 为谨慎起见对im做单位根检验(c,0,0): 表2 ADF Test Statistic -0.732387 1% Critical Value* -3.6852 5% Critical Value -2.9705 10% Critical Value -2.6242 可见,im在10%的显著性水平下也不能通过检验,序列存在单位根。 对数据做一阶差分,令dim=im-im(-1),对dim做折线图: 附图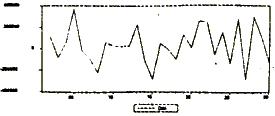 图2 由图2可见,一阶差分后,dim已经消除了趋势,做单位根检验(c,0,0): 表3 ADF Test Statistic -3.863289 1% Critical Value* -2.6522
图2 由图2可见,一阶差分后,dim已经消除了趋势,做单位根检验(c,0,0): 表3 ADF Test Statistic -3.863289 1% Critical Value* -2.6522