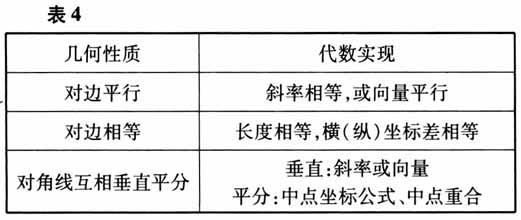
史宁中教授指出，创新能力的培养依赖于三个方面：知识的掌握、思维的训练、经验的积累.《普通高中数学课程标准（2017年版）》（以下简称《标准》）将“四基”纳入课程目标，首次在《标准》中提出“数学基本活动经验”是数学学习的基础，但是一线教师对“数学基本活动经验”在哪里并不清楚，因此迫切需要形成各知识模块基本活动经验的分布索引.只有这样，才能将课程目标细化，提出不同阶段学生积累数学基本活动经验的发展目标. 本文将“几何特征代数化”列举为高中生在学习解析几何课程时必须积累的基本活动经验，描述内涵、梳理内容、分析价值. 一、对数学基本活动经验的理解 1.数学基本活动经验的内涵 数学基本活动经验至今尚无统一的定义，综合已有的研究成果，我们将数学基本活动经验界定为：在数学目标的指引下，经历观察、操作、思考等数学活动过程，由感性向理性飞跃时形成的能有效指导学生相关数学活动、促进学生认知发展的认识、体验与观念.它本质上是形成一定的思维模式，建立一种数学直观. 2.基本活动经验的类型划分 专家们从不同的角度对数学基本活动经验进行了分类，有的按活动的类型分类，有的按学科分类，有的按所含的成分分类.有些分类比较笼统，对教学的指导作用不大，而有的分类教师又难以理解和掌握.这里我们借鉴向立政老师的研究成果，将数学基本活动经验划分为事实性经验、程序性经验和策略性经验. 事实性经验指的是能反映客观事实的经验.例如，公式、法则、规律、原理等. 程序性经验指的是能反映某类问题解决的一般程序或步骤的经验.例如，技能、算法、技巧和方法等.策略性经验指的是能反映认知策略方面的经验（包括元认知）.例如，策略、反思、交流等. 二、“几何特征代数化”经验的内涵描述与类型划分 1.内涵描述 解析几何的学科基本思想是用代数的方法研究几何问题，采用的方法是坐标法.就是通过建立坐标系，使平面内的“点”对应“有序数对”，从而建立起几何图形与方程之间的联系，再通过代数的方法研究方程，实现研究几何图形性质的目的.因此，解析几何问题必须首先将题目条件或结论中的几何特征（角、线段长度、斜率、面积等）转化成代数形式.转化的策略主要有：（1）几何特征直接代数化，即“直译”；（2）先把几何条件用几何方法进行适当地分解或处理，再代数化，即对难以“直译”的条件先利用平面几何知识“转化”为“简单、易翻译”的条件后，再进行“直译”. 这种转化在几何与代数之间架起了一座沟通的桥梁，从而实现对几何性质从定性到定量的研究，达到对图形性质更精细的把握.同时，也拓宽了几何学研究的视角.在此基础上形成的坐标法与综合论证法、向量法、分析法共同构成中学数学研究几何图形性质的四大方法，完善了学生的认知结构. 2.类型划分 由于该经验反映的是不同数学语言相互转化的思维策略，因此我们将“几何特征代数化”活动经验的类型界定为策略性经验. 三、内容梳理 以下对中学平面解析几何课程中常见的“几何特征代数化”经验进行梳理. 平行四边形条件的转化如下页表1所示.
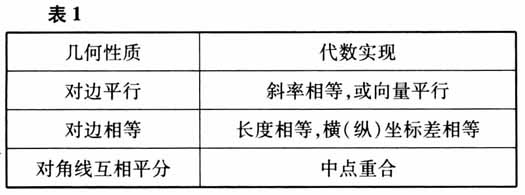
直角三角形条件的转化如表2所示.
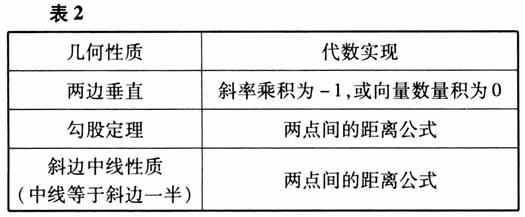
等腰三角形条件的转化如表3所示.
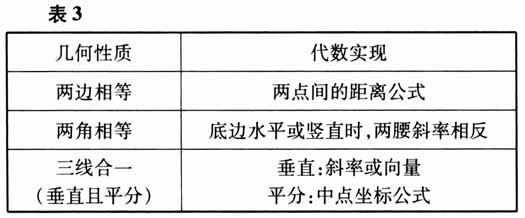
菱形条件的转化如表4所示.
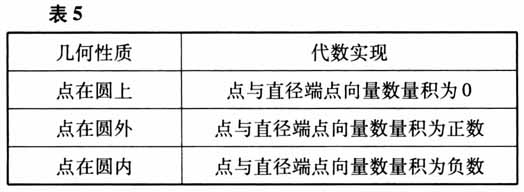
圆条件的转化如表5所示.
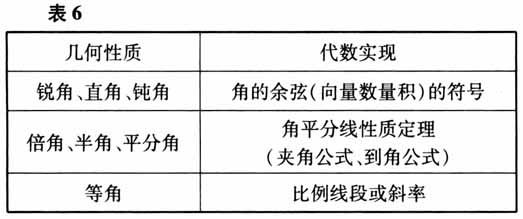
角条件的转化如表6所示.
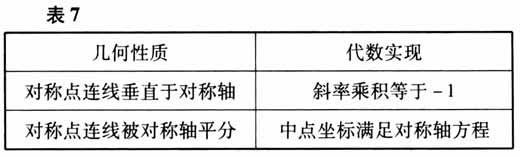
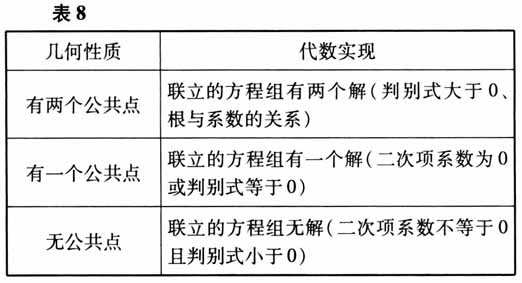
轴对称条件的转化如表7所示. 直线与圆锥曲线公共点个数条件的转化如表8所示.
