美国高校价值观教育路径研究

      目前教师都有意识地进行探究式教学，但效果迥异，最大的原因在于不能选择适切的探究策略.所谓适切，就是要针对教学内容、针对学生实际，采用相应的探究方法.总的原则是要考虑学生的发展，要有利于提升学生的学科素养，要更多地从有利于促进“学”的角度去设计教学，而不是一味地考虑如何便于教.笔者结合教学实践，总结了四大类的探究策略：整体类比法、归纳推理法、演绎推理法、变式递进法.下面结合课例来阐述具体方法以及它的适切性.

      一、整体类比法

      整体类比法一般适合前后内容相似或相近的教学.如指数函数与对数函数，等差数列与等比数列，椭圆与双曲线等，学完前一节的内容，进入下节学习时，可以引导学生类比上一节课，自行尝试探究，交流展示，教师引导提升总结.这样的方式有利于学生抓住问题本质，也能学会运用类比来研究数学问题，遇到相关联的内容时，教师大多都能采纳这样的教学方式.

      笔者曾大胆尝试做了章与章之间的类比探究教学.在开设空间向量章首课时，让学生先回顾平面向量所学的知识和研究方法，由此类比联想空间向量可以研究哪些内容，思考哪些定理可以从平面拓展到空间.

      教学中，学生较好地把许多知识要点作了类比推广，但纠结于平面向量基本定理如何向空间推广，教师启发学生思考：平面向量基本定理的本质是什么？一番研究探讨之后，学生尝试着把该定理向空间作推广.教师追问：这样的推广正确吗？逼迫学生深入思考.由此，掀起了又一波探究学习的热潮，而随后的学生展示与争辩让课堂精彩纷呈.

      应该说，章与章之间的整体类比探究，既打破了常规教学，更让我们欣赏到了学生不一样的精彩.这其中，学生不仅习得了知识和方法，更大力提升了他们的学科素养.

      二、归纳推理法

      此处的归纳往往指不完全归纳，即对于研究一般性的结论比较困难的数学问题，不妨从特殊情形入手，等寻求到了有效解决策略后，再去尝试推广.一般适合研究蕴含规律性的数学问题.数列中的一些公式、性质等适合用此法来研究.如等差数列的通项公式，等比数列的求和公式等，从特殊项去探寻规律，进而猜测一般性的结论，最后辅以严格论证.

      下面以等比数列求和公式为例，来阐述如何应用归纳推理法.

      首先回顾分析等差数列求和公式，其前n项和与哪几个量有关，从而可类比得出等比数列求和公式应该也与首项、公比、项数或末项有关.那么如何探寻这个关系式呢？

      学生尝试探究，发现等差数列的倒序相加法在此失效，但剖析等差数列求和公式，可发现其蕴含的普遍性，即对n的任何取值均成立，暗示着要探寻等比数列求和公式，不妨从特殊项入手去探寻研究.

      一番探究后，学生列出了如下一串等式：

      

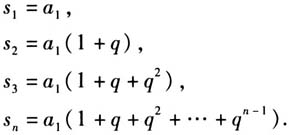      面对这一串等式，大家认同其有规律，但要成为公式，必须要简化，如何简化亟待研究.

      学生探究一番后没有头绪，于是教师提醒到：大家以往几乎没有接触过把一长串和简化成几项的形式，但大家一定尝试过把一个多项式变成两个多项式的积，这种方法称之为什么？

      教师话音刚落，就有学生联想到是因式分解，而现在是要把任意多项转化成少数项，那如何实施呢？

      顺着这一思路，学生探究发现对于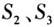，两个等式，两边同乘以1-q，就可以逆向利用平方差和立方差公式，把右边多项和转化成为两项差的形式.

      但对于后续的等式，尤其是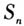，学生不敢妄下结论，因为之前没有学过n次多项式的因式分解，但教师鼓励学生去尝试展开计算.

      

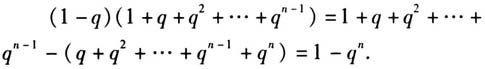      规律终于呈现，学生自是非常高兴.而这样的一个演绎探究过程，虽一波三折，但顺应了学生的思维发展，教师只在关键处点拨启发，使得探究真正地发生.

      三、演绎推理法

      为了研究一个相对复杂的性质或定理，先从它的外延入手、层层演绎递进，最后触及其核心.运用好演绎推理首先要理清研究内容的本质，弄清学生学习该内容存在的难点或混淆点，然后在此基础上再设计具有导引性的问题串，最后揭示其本质.下面以直线的斜率为例来阐述.

      苏教版必修2对于直线斜率有这样一段描述：

      楼梯或路面的倾斜程度可以用坡度来刻画，那么可以用类似的方法来刻画直线的倾斜程度，由此就可以得出斜率的坐标公式.

      显然，教材省略了得到公式的演绎推理过程，教师如果不加引导探究，学生只能是依葫芦画瓢，知其然而不知其所以然.但这一过程是教学难点，在关于这节课的许多公开教学中，教师也想让学生通过探究得到公式，但往往浅尝辄止.在给出坡度公式之后，让学生去凭空猜想，若学生猜不出，就直接告知；若能猜出，不去进一步追问缘由.这样的探究只能流于形式.