巩固社会主义核心价值观认同的道德基础

      《普通高中数学课程标准（2017年版）》中指出：“高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质.”[1]如何上好一堂指向高中数学核心素养下的数学概念教学课，让学生真正理解概念的内涵、研究对象的要素，引导学生把握数学内容的本质，引发很多一线教师的思考.

      近期，笔者有幸代表浙江省参加了第九届全国高中青年数学教师优秀课观摩与展示活动，这次参赛的课题是中国教育学会中学数学教学专业委员会自选课题“函数的周期性”，它是以人教A版必修4第一章第四节为蓝本，本节课的学习从周期性现象出发，开启数学学习之旅.笔者对于“函数的周期性”这节课的教学策略进行探讨.

      一、教学实践

      （一）情境引入

      问题1 现实生活中有哪些周而复始的现象？

      数学源于生活，而又高于生活.这节课的引入就从同学们身边熟悉的课程表开始，用心观察，生活中处处有数学.为了让学生充分感受周而复始的现象，在课前安排了数学学习小组查阅相关资料，在课内安排了两个学生活动：学生举例；数学学习小组代表上台进行展示分享.让学生们了解到大到天体的运行，小到质点的运动，生活、物理、数学中存在大量周而复始的现象.

      地球自转引起的昼夜交替变化；月亮圆缺变化，即朔—上弦—望—下弦—朔；潮汐变化，即海水在月球和太阳引力作用下发生的周期性涨落现象；物体做匀速圆周运动时位置变化的周期性；做简谐运动的物体的位移变化；交变电流随时间的变化情况，电流值也是重复出现的.

      地球绕日公转轨道是一个接近正圆的椭圆，每经过一年地球围绕着太阳转一周.在一年内，日地距离都在不停地变化中.无论从哪个时刻t算起，经过一年时间，地球又回到原来的位置，所以地球与太阳的距离是周而复始变化的.

      

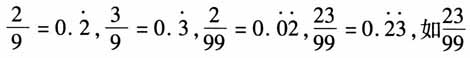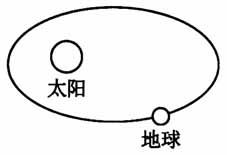
      循环小数：，小数点后2，3依次重复出现.

      水车上A点到水面的距离为y，假设水车5min转一圈，那么y的值每经过5min就会重复出现，因此距离y随时间的变化规律是周而复始变化的.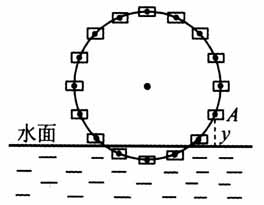

      

      （二）概念生成

      问题2 如何用数学的方法来刻画现实世界中周而复始的现象？

      在小组代表所举的例子中，选取了三个典型的例子：天体的例子，数学中的例子，生活中的例子.

      如何进行数学抽象？

      随着时间的变化，地球与太阳的距离（日地距离）发生变化.在任何一个确定的时刻t，日地距离s是唯一确定的，因此距离s是关于时间t的函数.在现实世界中，借助变量观点，构造函数s=f（t），进一步借助函数关系式刻画周而复始的变化规律.地球每经过12个月，又回到原来的位置，在关系式上的表达：f（t+12）=f（t）.

      小数点后的第n位的数字作为这个函数的函数值，记作y=f（n）.可写成分段函数的形式，f（n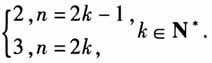）=用函数的关系式来刻画循环小数出现周而复始的现象，即f（n+2）=f（n）.循环小数的循环节的长度为2，自变量每增加2，函数值会重复出现.

      水车上A点到水面的距离呈现周而复始的现象，这给我们似曾相识的感觉，当初我们定义正弦函数，就是类似这个背景.正弦函数是以角x为变量，角的终边与单位圆的交点纵坐标为函数值的函数.选用有向线段MP表示正弦线.

      角逆时针方向转动一圈，正弦函数值重复出现，即自变量增加2π，正弦函数值会重复出现，即正弦线的长度和符号均没有发生变化.用式子来描述，sin（x+2π）=sinx，x∈R，这也是正弦函数的诱导公式.可以抽象成一般函数的形式f（x+2π）=f（x）.角继续逆时针方向转动或者顺时针方向转动，正弦函数值重复出现，当自变量的值每增加2π的整数倍时，正弦值会重复出现，即sin（x+2kπ）=sinx，x∈R.可以抽象成一般函数的形式：f（x+2kπ）=f（x）.

      

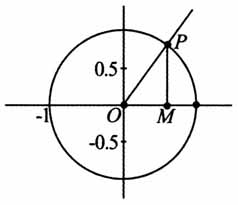      对于现实世界中的周而复始现象进行数学抽象，与学生共同构造函数，进一步地利用函数关系式，刻画周而复始的现象.在这一过程中，需要学生用数学语言表达问题、用数学知识与方法构建模型，培养学生数学建模素养.

      问题3 你能否给出周期函数的定义？

      一般地，对于函数f（x），如果存在一个T，满足f（x+T）=f（x），那么函数f（x）就叫做周期函数，T叫做这个函数的周期.此时学生形成的定义并不完善，与学生共同建构定义.