武汉大学机构用户，欢迎您！
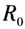与世代间隔T，通过统计模型描述在一定时期内累计感染病例数随时间的变化规律.试题就模型的一个应用——估计病例数增加一倍需要的时间而设问，既考查相关的数学知识和从资料中提取信息的能力，又突出数学和数学模型的应用.从模型来看，在疫情初始阶段没有采取防控措施的情况下，疫情传播速度是非常快的，感染病例呈指数增长，感染病例数平均1.8天增加一倍.通过对试题的求解，学生能够了解传染病的传播规律，感受我国为世界疫情防控所作出的努力，体会党和国家及时采取科学、精准、严格的防控措施的重大意义. 二是用数学模型揭示疫情遏制阶段的规律.全国Ⅲ卷文、理科第4题以新冠肺炎疫情传播的动态研究为背景，选择适合学生知识水平的Logistic模型作为试题命制的基础，考查学生对指数函数基本知识的理解和掌握，以及使用数学模型解决实际问题的能力.试题的情境和数学模型对疫情预测和精准防控具有重要的指导意义.试题情境真实，素材取自于学者基于实际数据的研究成果，相关具体参数真实可靠，试题的设定和提问有充足科学依据，坚持命制应用性试题的基本原则，体现科学性与时代性的结合. 上述2道试题充分体现应用性试题贴近时代、贴近社会、贴近生活的特点，考查数学建模和数学应用能力，鼓励学生探索真理、以自己的科学知识为人类社会服务. （二）展现中国抗疫成果 全国疫情防控进入常态化后，各地有序推进复工复产复学.新高考Ⅱ卷第9题以复工复产为背景，取材于某地复工复产指数的真实数据，考查学生解读统计图以及提取信息的能力.试题从人民群众关切的国计民生问题出发，根据真实数据编制折线图，简单、直观、清晰地显示复工复产情况.通过对复工复产指数的分析，展示我国新冠肺炎疫情防控取得的成果，体现立德树人的教育理念，同时引导中学加强数学应用素养的培养，提高数学应用意识和应用能力. （三）体现志愿精神 全国Ⅱ卷理科第3题（文科第4题）是以志愿者参加某超市配货工作为背景设计的问题，考查学生对基本知识的掌握程度及运用所学知识解决问题的能力.试题背景是疫情期间大规模的网购、配货，是发生在学生身边的真实事情，学生十分熟悉.试题考查的知识和方法都很基本，学生只要读懂试题内容，运用概率的基本知识即可求得问题的答案，对学生提高获得感及稳定考试心态都有良好的作用.试题考查学生分析问题和解决问题的基本能力，体现了对核心素养与关键能力的考查.试题的情境具有时代性，体现志愿精神，具有积极的教育意义. 二、突出理性思维，考查关键能力 数学在人类社会发展中起着十分重要的作用，数学实力已经影响着一个国家的综合实力.站在立德树人的高度审视数学教育，数学素养影响人的长远发展，数学素养的教育在培养学生真、善、美的品质和创造力方面有着特殊和重要的作用. 理性思维在数学素养中起着最本质、最核心的作用.高考数学突出理性思维，将数学关键能力与理性思维、数学应用、数学探究、数学文化的学科素养统一到理性思维的主线上，在数学应用、数学探究等方面突出体现理性思维和关键能力的考查. （一）考查批判性思维能力 批判性思维是重要的能力素养，是理性思维的高度体现，批判性思维的培养对于培养人的优良品质与创造力具有重要的意义.高考数学突出对批判性思维能力的考查，考查学生推理论证、发现错误、修正错误的能力，以及发现解决问题的方向和方法的能力[2].全国Ⅰ卷理科第12题通过创新设计，考查学生对指数函数与对数函数的单调性、指数幂的运算、对数运算与换底公式等知识的灵活运用.题目中的未知量关系不能简单地用初等函数表示出来，需要运用指数函数与对数函数的知识对题设条件进行恒等变形，将不同形式表示的量转化为同一类型的表达形式，由此实现对批判性思维能力的深入考查.全国Ⅱ卷理科第16题以立体几何基础知识为背景，设置4个命题，并使用简单的逻辑连接词，构造4个复合命题，要求学生判定这些复合命题的真假.试题将立体几何的问题与逻辑命题有机结合，多侧面、多层次考查学生对立体几何和逻辑知识的掌握情况；试题进一步要求对立体几何命题、复合逻辑命题进行逐个、双重判定，并且要求选择所有的真命题，不能遗漏、不能有误，对批判性思维能力的考查提出新的更高要求.
