马克思主义批评理论的初始形态

      立体几何是高中数学的重要内容之一，主要研究现实世界中物体的形状、大小与位置关系.其中，探究多面体的截面画法是利用点、直线、平面基本图形位置关系的核心知识，推理论证多面体的结构特征，培养学生几何作图的方法与技能.同时，也是利用作图表达概念的内涵，加深学生对定义、公理、定理等理论知识的理解，提升直观想象、数学抽象、逻辑推理等数学核心素养，逐步建立空间观念的关键一环.多面体截面就是用一个平面去截这个多面体得到的平面图形.在解决立体几何的相关问题中，常常需要借助或转化为平面几何的问题，从而确定平面是这一转化的重要条件.因此，在认清构成多面体点、线、面位置关系的基础上，需要在多面体中画出截面图形.本文通过四种策略探究多面体截面的画法.

      一、直接转化法

      当用一个平面截多面体，画出截面图形时，时常把直线与平面的位置关系转化成直线与直线的位置关系，寻找到平面与多面体的棱相交的截点的位置，然后依次连接截点即可.常见于实物模型，渗透了解决立体几何问题常用而有效的化归思想方法.

      例1 如图1所示的一块木料中，棱BC平行于面A′C′.要经过面A′C′内的一点P和棱BC将木料锯开，应该怎样画线？

      解析：过点P和棱BC将木料锯开，实际上就是过点P和棱BC确定一个平面，即过已知直线BC和点P作一个平面与已知平面A′C′相交.根据直线与平面平行的性质定理和公理4可知，在平面A′C′内，过点P的直线EF与直线B′C′平行，作出的平面FEBC就是所确定的平面，如图2所示.则EF，BE，CF就是所画的线.

      

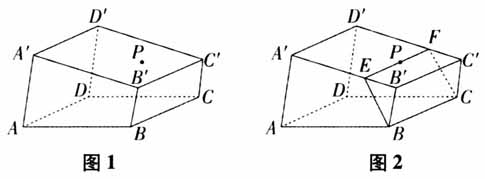      例2 设四棱锥P-ABCD的底面不是平行四边形，用平面α去截此四棱锥，使得截面四边形是平行四边形，则这样的平面α（

       ）.

      （A）不存在 （B）只有1个

      （C）有4个 （D）有无数多个

      

      

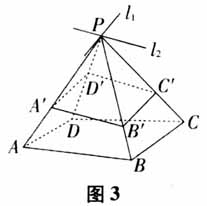      可见这样的平面α有无数多个，故答案选D.

      【评析】例1的解答中，有的学生可能会思考，过点P直接作棱BC的平行线不是更加简捷吗？教学中只需要让学生自己动手在一个实物模型中画一画，就可以消除学生对这个问题的疑虑.另外，利用例2把学生的思维引导到用直线与平面平行的性质定理解决交线问题，将直线与平面的平行问题化归为直线与直线的平行问题，再通过直线与直线平行来判定直线与平面平行的问题，渗透了常用而有效的化归思想.

      二、延展法

      空间体中，如果棱上的截点位置无法直接确定，常常需要借助局部截面的延展与多面体每个面上的两个交点的连线来确定截面图形.一般情况下，选择延伸截面内的直线与多面体的棱或棱的延长线有交点更有利于画图.实际教学中，常常借助于这种延展法练习，加深对平面的三个公理的认识，提升研究空间几何图形问题时进行逻辑推理的能力.

      例3 如图4，正方体ABCD-A′B′C'D′中，E，F，G分别为AB，AD，B′C′的中点，那么正方体过E，F，G的截面图形是（

       ）.

      （A）三角形 （B）四边形

      （C）五边形 （D）六边形

      解析：如图5，作GP//EF交C′D′于点P（平面与平面平行的性质定理），在平面AC内延长EF，BC交于点R，连接GR交B′B于点M，连接EM.同理，在平面AC内延长EF，CD交于点Q，连接PQ交DD′于点N，连接NF.所以过点E，F，G的截面图形FEMGPN是六边形，故答案选D.

      

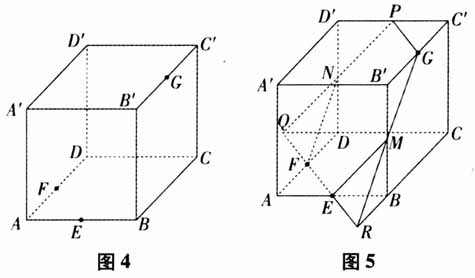      例4如图6，A′，B′，C′三点分别在四棱锥SABCD侧棱SA，SB，SC上，且SB′＞SA′，SB′＞SC′，试画出过点A′，B′，C′的平面截四棱锥S-ABCD的截面.

      解析：如图7，连接A′B′并延长与AB的延长线交于点N，连接B′C′并延长与CB的延长线交于点M，连接MN并延长与DC的延长线交于点P，连接C′P并延长与SD的延长线交于点D′，连接A′D′，则四边形A′B′C′D′就是所求截面图形.

      

      【评析】分别用在平面EFG内作平行线和在平面A′B′C′内作相交线的方法延展平面，将截面问题与已知概念和原理联系起来，引导学生通过深度学习挖掘平面图形与立体图形的内在联系，实现由认识平面图形到认识立体图形的飞跃.