我们处在教育改革的滚滚洪流中,素质教育、数学文化、慕课、翻转课堂、现代化教育技术,改革理念与措施层出不穷!我们是否认真思考过:为什么要改革?基础教育存在的根本问题是什么?我们应该关注课堂教学中的哪些方面,是外在的形式还是内在的思想? 弗赖登塔尔是荷兰著名的数学教育家,在代数拓扑与李群方面有过重要建树,30岁左右便开始关注数学教育.他在数学教育方面的论著很多,其《作为教育任务的数学》一书中有一个重要的观点广为熟知:“数学教育是数学的再创造.”无独有偶,美国著名的物理学家、诺贝尔奖获得者费曼也说了一句脍炙人口的话:“我不能创造的,我也无法理解.”他们的话说明了什么?教育不是简单的知识传授,而是思想的传播与创造力的激发. 本文试图针对目前中学数学教育中存在的若干问题做一个初步的探讨,期待能为教学教育改革与研究者及一线教师的教学提供一些可资参考的建议. 二、“阳春白雪”与“下里巴人” 阳春白雪与下里巴人本是战国时代的两支曲子,前者典雅高深,后者通俗易懂.后分别引申为高雅的文学作品与通俗的文学作品.两者针对的对象不同,无褒贬之分. 在我国,数学从来没有像今天这样,受到举国上下的关注与重视,大家都在高谈阔论数学与数学教育,对数学的热衷程度远超过20世纪80年代初的“陈景润时代”.不过,如今的“数学热”与那时有本质的不同,是从战略层面上的重视. 重视数学是个大好事,数学也的确应该被重视,它虽然不是万能的,但没有它却是万万不能的.然而,我们同时也应该清楚,作为战略层面上的数学,它注定是小众化的,不可能像万众创新、大众创业那样大家都来做数学.数学的功能大体可以分为两个方面:一是思维,二是运用.一个人一旦具备了数学思维与思辨能力,的确如虎添翼,受益终身.而从技术层面上看,很多技术研发的本质是算法的设计与运用.没有良好的数学思维能力与素养,很多事情确实做不了.当然,数学本身并不能带来经济效益,也不能带来科技产品,只有与其他领域相结合后才能看到它强大的威力! 我们知道,诺贝尔奖不设数学奖,但无论是和平奖、文学奖、经济学奖,还是物理学奖、化学奖、生理学或医学奖,没有一个奖项所在的领域缺过数学家.可见,数学具有相当的普适性.例如,罗素既是个哲学家也是个数学家,还是个文学家,他居然得了个诺贝尔文学奖!所以人们戏称:“没有得过诺贝尔文学奖的数学家不是个好的哲学家.” 面向普通大众的数学教育注定不可能是“阳春白雪”.从这个意义上说,数学教育应该分两个层次:一个层次是培养数学精英的“阳春白雪”,另一个层次则是面向普通大众的“下里巴人”.我们在强调数学重要性的同时也应该清楚,以数学研究与数学的深度应用为目标的数学教育必然是小众化的“阳春白雪”,大多数人应该接受的是“下里巴人”式的数学教育.问题是:谁来决定谁接受“阳春白雪”式的教育,谁接受“下里巴人”式的教育?如何实施?因为现实中,但凡有条件的父母都希望自己的孩子接受最优质的教育.我认为,最好的办法是降低日常教学的难度,加大高考试题的难度和梯度,尽可能杜绝单凭熟练度就可以得分的题目.同时,增加诸如AP课程(大学先修课程)的先修课,让有潜力的孩子学到更多更深入的数学——当然,不要让大多数孩子陪读.这并非什么创新举措.与西方不同的是,普通百姓不需要花重金进入私立学校读书,只要确有天赋,同样有脱颖而出的机会.当前,我们的优质教育资源毕竟是有限的,最终能进入“985”高校的学生不会超过5%.与其让所有孩子陷入白热化竞争的漩涡,不如通过自然淘汰的方式让真正优秀的孩子接受最好的教育.一些“漏网之鱼”进入普通高校后,还可以继续努力以求“翻身”. 三、数学史与数学课堂 数学课堂有一种理念叫HPM.数学课堂结合数学史是个好事,但我们不能误解数学史在课堂教学中的意义与作用,特别是落实到实操层面时,不能把它看成简单的数学史实的介绍,以为这就是在普及数学思想或数学文化了. (一)数学史在数学教育中的意义 数学史在数学课堂教学中的意义何在?是简单地引入数学史以增加课堂的趣味性,还是将数学史融入课堂教学过程中以体现数学的思想性?这是判断课堂教学是“拼盘式”还是“融合式”的重要标准.所谓“拼盘式”,指的是教师在讲授数学概念或原理时也介绍点数学史,但两者是割裂的,数学史仅仅当成故事来讲;所谓“融合式”,指的是将数学史上一个概念或原理的产生过程再现出来,概念教学的过程就是历史展现的过程,二者合二为一,形成一个整体(也称之为“数学的再创造”).然而,不是所有的教学都适合把历史真实重演一遍,教学也不必拘泥于历史的进程.教师熟悉数学史的目的和意义在于,可以抓住导致概念或原理产生的根本问题,并结合、参考学生的认知基础创设合适的问题情境来实现再创造,这才是渗透数学思想方法和文化的有效手段. (二)课堂教学不能离题万里 课堂教学引入数学史,并不意味着把数学课开成数学史课.例如教学复数概念,偏从数的起源讲起,洋洋洒洒讲了一堆自然数、有理数、实数、复数的历史,那就跑题了!复数就是复数,抛弃那个荒谬的方程
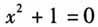
是一个进步,但卡尔丹公式远远不足以成为复数存在的理由,它只不过让数学家们对一些现象疑惑不解而已.虽然很多数学家包括欧拉都使用过复数(因为用它做形式演算并不会导致矛盾),但复数作为一个不可思议的“怪物”,在它出现在卡尔丹公式后的200年中始终未能在数学界掀起大的波澜,远不像无理数、无穷小、集合论的出现曾翻腾起数学界的惊涛骇浪.为什么一个
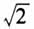
的出现会惹出一场轩然大波,以至于让希帕索斯为之命丧大海,而虚数的出现并未令数学家们惊慌失措,他们依然故我,优哉游哉地沉浸在实数的优美世界里?因为数学家们意识到,几何与有理数之间存在着不可调和的矛盾,
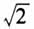
动摇了神一般存在的毕达哥拉斯学派的信仰!而复数并没有导致数学的根本矛盾,现实中也找不到虚数的影子.数学家们好奇的并非是虚数是否存在,而是它为什么虚无缥缈却又可以参与正常的运算而不会导致矛盾?卡尔丹并不认为虚数是有意义的,他说:“算术就是这样神妙地搞下去,它的目标,正如常言所说,是既精致又不中用的.”笛卡儿更是不认同虚数,虽然他的坐标系换一种方式便可以解释复数.但大多数的数学家并不排斥复数,因为它有时的确可以解决问题,正如莱布尼茨所说,“圣灵在分析的奇观中找到了超凡的显示,这就是那个理想世界的端兆,那个介于存在与不存在之间的两栖物,那个我们称之为虚的-1的平方根”.如果我们对复数的引入仅仅停留在卡尔丹公式,不再跨越那漫长的200年,走进物理与几何的世界,就不可能真正懂得复数的意义与价值,以及它对数学、物理学产生的深远影响,也不可能清楚复数的四则运算是什么,而只能像卡尔丹们一样将它理解成纯粹的形式运算,更不可能了解此后为什么会出现四元数甚至八元数.①
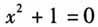 是一个进步,但卡尔丹公式远远不足以成为复数存在的理由,它只不过让数学家们对一些现象疑惑不解而已.虽然很多数学家包括欧拉都使用过复数(因为用它做形式演算并不会导致矛盾),但复数作为一个不可思议的“怪物”,在它出现在卡尔丹公式后的200年中始终未能在数学界掀起大的波澜,远不像无理数、无穷小、集合论的出现曾翻腾起数学界的惊涛骇浪.为什么一个
是一个进步,但卡尔丹公式远远不足以成为复数存在的理由,它只不过让数学家们对一些现象疑惑不解而已.虽然很多数学家包括欧拉都使用过复数(因为用它做形式演算并不会导致矛盾),但复数作为一个不可思议的“怪物”,在它出现在卡尔丹公式后的200年中始终未能在数学界掀起大的波澜,远不像无理数、无穷小、集合论的出现曾翻腾起数学界的惊涛骇浪.为什么一个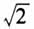 的出现会惹出一场轩然大波,以至于让希帕索斯为之命丧大海,而虚数的出现并未令数学家们惊慌失措,他们依然故我,优哉游哉地沉浸在实数的优美世界里?因为数学家们意识到,几何与有理数之间存在着不可调和的矛盾,
的出现会惹出一场轩然大波,以至于让希帕索斯为之命丧大海,而虚数的出现并未令数学家们惊慌失措,他们依然故我,优哉游哉地沉浸在实数的优美世界里?因为数学家们意识到,几何与有理数之间存在着不可调和的矛盾,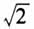 动摇了神一般存在的毕达哥拉斯学派的信仰!而复数并没有导致数学的根本矛盾,现实中也找不到虚数的影子.数学家们好奇的并非是虚数是否存在,而是它为什么虚无缥缈却又可以参与正常的运算而不会导致矛盾?卡尔丹并不认为虚数是有意义的,他说:“算术就是这样神妙地搞下去,它的目标,正如常言所说,是既精致又不中用的.”笛卡儿更是不认同虚数,虽然他的坐标系换一种方式便可以解释复数.但大多数的数学家并不排斥复数,因为它有时的确可以解决问题,正如莱布尼茨所说,“圣灵在分析的奇观中找到了超凡的显示,这就是那个理想世界的端兆,那个介于存在与不存在之间的两栖物,那个我们称之为虚的-1的平方根”.如果我们对复数的引入仅仅停留在卡尔丹公式,不再跨越那漫长的200年,走进物理与几何的世界,就不可能真正懂得复数的意义与价值,以及它对数学、物理学产生的深远影响,也不可能清楚复数的四则运算是什么,而只能像卡尔丹们一样将它理解成纯粹的形式运算,更不可能了解此后为什么会出现四元数甚至八元数.①
动摇了神一般存在的毕达哥拉斯学派的信仰!而复数并没有导致数学的根本矛盾,现实中也找不到虚数的影子.数学家们好奇的并非是虚数是否存在,而是它为什么虚无缥缈却又可以参与正常的运算而不会导致矛盾?卡尔丹并不认为虚数是有意义的,他说:“算术就是这样神妙地搞下去,它的目标,正如常言所说,是既精致又不中用的.”笛卡儿更是不认同虚数,虽然他的坐标系换一种方式便可以解释复数.但大多数的数学家并不排斥复数,因为它有时的确可以解决问题,正如莱布尼茨所说,“圣灵在分析的奇观中找到了超凡的显示,这就是那个理想世界的端兆,那个介于存在与不存在之间的两栖物,那个我们称之为虚的-1的平方根”.如果我们对复数的引入仅仅停留在卡尔丹公式,不再跨越那漫长的200年,走进物理与几何的世界,就不可能真正懂得复数的意义与价值,以及它对数学、物理学产生的深远影响,也不可能清楚复数的四则运算是什么,而只能像卡尔丹们一样将它理解成纯粹的形式运算,更不可能了解此后为什么会出现四元数甚至八元数.①