科学陈述教学目标 谢发超在《导向深度学习的数学教学目标设计——以“函数的单调性”为例》一文中指出,在深度分析课程标准、教材内容、学生的基础上还需要将这些粗浅的、分散的教学目标科学地整合到一起,用恰当的方式表达出来,才能使确定的目标有效地导引学生深度学习.以“函数的单调性”为例,教学目标的初步建构为: (1)能从形与数两方面理解函数单调性的概念.(2)初步掌握函数单调性的证明方法.(3)经历从具体到抽象、从特殊到一般、从感性到理性的认识函数单调性的过程.(4)通过对函数单调性概念的探究,培养自己观察、归纳、抽象的能力和语言表达能力.(5)通过对函数单调性的证明,提高自己代数推理论证能力.(6)通过对函数单调性概念的探究,培养合作交流的意识和大胆猜想、乐于探究的良好品质. 上述教学目标本质上是以“三维目标”的方式进行表述的,未能充分体现达成该目标所需的条件与方式,显得比较空泛.在高一阶段,学生将在初中经验感知的基础上,通过图形化理解、关系化理解、离散化理解三个层次来理解函数单调性的概念.具体而言,需要经历“感知”“想象”“概括”“固化”“应用”“结构”六个环节.通过这样的分析,教师不仅再次梳理自己初步预设的教学目标是否准确、合理,还能思考教学目标达成是否有可落实的具体活动,是否具有促进目标达成的条件支持,避免教学目标实际达成过程中的虚设或落空.接着需要将教学目标科学、准确地表达出来.当前,课堂教学目标的陈述方法主要包括马杰行为目标陈述法、格伦兰内外结合陈述法和艾斯纳表现目标陈述法.三种方法各有优劣,因此,在实际操作中要灵活选择陈述技术,找到最合适的表达方式.经过调整后,教学目标为: (1)结合一次函数、二次函数,说明函数的变化趋势(理解层次).(2)能借助具体函数的图象直观,经历符号化过程,抽象出函数的单调性概念(分析层次).(3)能利用函数图象写出函数的单调区间,能利用定义证明一次、二次函数和反比例函数在某个区间的单调性(应用层次).(4)积极参与同学间、师生间的交流活动,知道符号化表达数学定义的意义,体会数学概念学习的基本方法(评价层次). 摘自《中小学教师培训》2019.1 如何细化教学目标 邵肖华等在《细化课堂教学目标,促进数学知识落实——两节公开课的实录与反思》一文中指出,细化课堂教学目标可以让课堂教学目标对教师的课堂授课具有切实的指导作用,可以让数学课堂教学目标的“具体化”“可操作”“可检测”得到真正实现.以“椭圆及其标准方程(第一课时)”为例,试讲课和公开课1的课堂教学目标主要关注:通过经历椭圆方程的化简,增强学生战胜困难的意志品质,并体会数学的简洁美、对称美.公开课2的教学目标主要关注:通过椭圆标准方程的推导过程,巩固用坐标化的方法求动点的轨迹方程,同时体会含有两个根式的化简思路.这两个课堂教学目标具有针对学生动手的操作性,但没有涉及曲线与方程关系中的核心问题,都没有对“什么是椭圆方程”这一教学目标进行细化.通过分析课程目标的要求、章节教学目标的要求、学生的学情,提出了细化后的教学目标:(1)动手画椭圆,根据两定点间距离与距离和之间的关系理解椭圆的定义;(2)通过对椭圆方程的化简与整理过程,利用完备性的说明,促进学生理解什么是椭圆方程、为什么
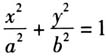
(其中a>b>0)是椭圆的标准方程;(3)借助简单练习,强化椭圆两个不同标准方程的差异,能求椭圆的标准方程. 摘自《中学教研(数学)》2019.6
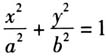 (其中a>b>0)是椭圆的标准方程;(3)借助简单练习,强化椭圆两个不同标准方程的差异,能求椭圆的标准方程. 摘自《中学教研(数学)》2019.6
(其中a>b>0)是椭圆的标准方程;(3)借助简单练习,强化椭圆两个不同标准方程的差异,能求椭圆的标准方程. 摘自《中学教研(数学)》2019.6