清政府为了解全国各地粮食供需状况，规定各级地方政府定期向上级报告辖区内的雨雪量、收成、粮价、人口和仓储积谷情况，建立了全国性粮价奏报制度。这些粮价资料地域上涵盖了中华帝国的所有省份，时间上长达近两个世纪，为当代经济史学者提供了大量基础数据。自20世纪80年代起有学者运用数理统计方法对粮价资料进行量化分析，以考察当时的粮食供需情况、市场区域划分、市场发育程度等问题。这类研究主要集中在两个方面：第一，对粮价这一时间序列的变动进行分析；第二，利用不同市场间价格变动的同步性，研究市场整合问题。 一、数据类型与遗漏值补全 按照被描述的对象与时间的关系，可以将统计数据分为截面数据和时间序列数据。时间序列数据指在不同时间上收集到的数据，它所描述的是现象随时间而变化的情况。截面数据指在相同或近似相同的时间点上收集的数据，描述现象在某一时刻的变化情况。面板数据，也叫“平行数据”或“时间序列—截面数据”，指在时间序列上取多个截面，在这些截面上同时选取样本观测值所构成的样本数据，是截面数据与时间序列数据的综合。从清代粮价研究的发展可以看出，民国时期的研究论著，主要贡献在于资料的发现和整理方面，对于数据的分析较少。①之后，粮价研究人员开始关注粮价长期趋势及变动原因、短期粮价波动、粮价变动的社会影响等问题，主要集中于对时间序列数据或截面数据的研究。代表性的有：全汉昇与王业键合作的《清雍正年间(1723-35)的米价》，详细列出了江苏、浙江、广东等12个中南部省份的米价及指数，得出雍正年间米价未长期上升、社会经济相当稳定的结论。②全汉昇与克劳斯(Kraus)比较了1713-1719年苏州米价与1913-1919年上海米价的季节性变动，结果二者相差不大，可知清代中期市场机制的发展已相当成熟。③岸本美绪对江南物价进行了大量细致研究，在《清代前期江南的米价动向》④和《清代前期江南的物价动向》⑤中，整理了明末至清前期江南的米、棉花、生丝、棉布、田地及工资价格表，这些价格均呈现出上升——下跌——高涨的变动趋势，并指出这一现象的产生源于人口、生产量、货币流通量等的综合影响。 20世纪80年代，有研究者开始将时间和空间两个维度结合。李中清的博士论文中最早出现了利用18世纪云南、贵州两省的粮价数据进行的市场整合研究。⑥薛华(Shiue，C.)的博士论文《中华帝国晚期的粮食交易和储存》，首次建立面板模型，运用回归分析，考察了收成丰歉等对18世纪中部和东南地区10个主要省份粮价的影响。⑦ 由于粮价数据中部分月份原件散失，因此，资料不完整是难以避免的问题。在进行数理统计分析之前，研究人员必须采取一定的方法将遗漏值补全。李中清在补入西南地区缺失数据时，假定缺失的价格作为一个平均价格因子，依据整个时期的月平均价及相邻月份的市场流通价格，对其作出估算。⑧陈春声在研究清中叶各府州米价季节变动指数时，用“线性插值法”对缺失数据做了增补。⑨王业键等采取非参数回归分析法(无母数回归分析法)补全资料遗漏的部分。⑩由于两点之间的近似随着所近似函数的二阶导数的增大而逐渐变差，因此函数的曲率越大，简单线性插值近似的误差也越大，此时用非参数回归分析法补全数据更准确一些。但当仅有个别数据缺失、在总数据中所占比例非常低时，以上几种方法都是可以接受的。 二、粮价趋势、季节性变动及周期循环 时间序列的构成要素分为四种，即趋势、季节变动、周期性或循环变动、随机性或不规则波动。就粮价的时间变动来说，研究人员最关心的三点是粮价趋势走向、周期循环和季节性变动。分析时间序列，多采用分解法，将原始资料依照需要分解的因素，转化成时间序列的分解模型。一般可分解为加法模型和乘法模型的简化形态。 濮德培(Peter C.Perdue)的《清政府和甘肃谷物市场：1739-1864》采用加法分解模型分析粮价长期趋势、季节波动、灾荒、战乱、政府和士绅平粜等因素对粮价变动造成的影响。(11)其公式是：
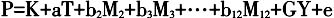
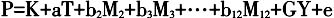其中，P为某月价格，K为常数，a为年份T的系数，b为除一月份(基期)外月份M的变数，G为灾荒、战乱年Y的系数(有灾害年G=1，无灾害年G=0)。用此公式可找出由于人口和通货膨胀造成的物价长期变动对价格的影响a，季节变动的影响b，灾害年的影响G。李明珠(Lillian M.Li)建立了类似的加法模型分析直隶谷物市场。(12)两人的研究均指出，省内价格波动的相互关联性高，长期变动、季节变动、灾害年三者影响都不大。当然，甘肃省有庞大的军事力量；宫廷、旗人、军事力量对直隶谷物市场的干预也非常普遍。因此，二者的市场整合程度高，可能是基于大规模政府干预而非真实市场的作用。 王业键等则在《十八世纪苏州米价的时间序列分析》(13)、《十八世纪东南沿海米价市场的整合性分析》(14)中，将原始资料转化成时间序列的乘法分解模型来进行分析。用公式表达为：
