文学事件不能只归于策略

      一、课程背景与意图

      《普通高中数学课程标准（2017年版）》在内容标准部分，将数学探究、数学建模与数学文化作为独立的部分呈现，阐述了各自的内涵、教育价值，并提出了要求，对如何实施给出了说明和建议.数学探究、数学建模作为一种新的学习方式引入高中数学课程，旨在为学生提供自主学习、探究学习的空间，使学生经历数学概念、结论产生的过程，体验数学在解决实际问题中的价值和作用，形成积极向上的情感、态度和价值观.[1]

      苏教版教材中有一类“操作题”，为学生提供了动手操作的素材，为学生体验数学知识的创造过程提供了可能，并能极大地提高学生学习数学的兴趣，培养学生的动手能力、思考能力和创新能力.为了利用好这一课本资源，同时降低学生学习椭圆的门槛，这就要求我们在课堂教学中重视学生的动手操作和观察思考层面的训练，从而加深学生对数学概念内在本质的理解，提升课堂教学的效果.为了贯彻苏州市教育系统落实拔尖创新人才培养相关要求，尊重青少年身心发展规律，关注青少年发展的多样性、差异性，为各类具备拔尖创新潜质的青少年提供适切的教育，在此探索过程中笔者面向本校拔尖学生开设了本次公开课.

      二、教学过程

      本次探索实验课通过实验与猜想、验证与结论、理解与应用、拓展与思考、总结与反思这五个环节，让学生充分发展“四能”，围绕问题展开，不断解决原有问题并提出新问题，环环相扣，最终使学生真正掌握问题探究的基本方式.

      ·环节1：实验与猜想

      师：准备一张圆形纸片，在圆内任取不同于圆心的一点A，将纸片折起，使圆周过点A，然后将纸片展开，就得到一条折痕l（为了看清楚，可把直线1画出来，如图1）.这样继续折下去，得到若干折痕，观察这些折痕围成的轮廓，它是什么曲线？大家两两分组配合完成.

      师：当我们折叠时，是否圆周上每一点都可以与点A对应产生折痕呢？

      生1：可以.

      师：既然可以，想象一下得到的图形是否封闭？

      生2：是封闭图形.

      师：因此当我们折叠次数尽可能多，大家猜测所围成的封闭图形是什么呢？

      生众：猜测是椭圆.

      师：接下来通过计算机模拟得到比较稠密的折痕，大家直观感受一下图2所围成的轮廓以及折痕与曲线的位置关系.

      

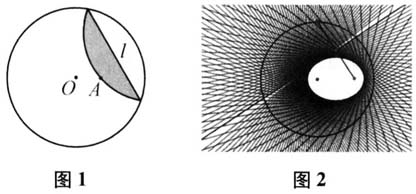      设计意图 在折纸实验观察轮廓线的过程中获得感性认识，在教师逐步追问后形成基本认识，从而猜测轮廓线为椭圆.正如张奠宙先生提出的，通过对具体事物进行实际操作、考察和思考，从感性认识向理性认识飞跃，形成基本数学经验.[2]

      ·环节2：验证与结论

      师：既然猜测轮廓线是椭圆，那么如何验证呢？

      生3：从图3中我猜测折痕应该与曲线相切，也是切线.

      

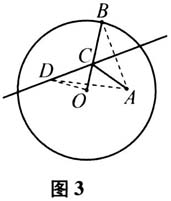      师：很好！请问如何说明折痕为切线，曲线为椭圆呢？

      生4：椭圆的切线即为与椭圆有且仅有一个公共点的直线，故可以从这个角度入手，找寻切点.

      师：很好！切点既在折痕上又在椭圆上，如何在图3中作出来？

      生5：折痕就是AB线段的垂直平分线，连结OB与折痕的交点记为C，只需证两件事：（1）点C在椭圆上；（2）折痕与椭圆有且仅有一个公共点.

      师：非常好！这两件事如何证明？

      生5：由垂直平分线的性质有CO+CA=CO+CB=OB（半径），且OA＜OB（半径），根据椭圆定义可知点C在椭圆上.任取折痕上的一点D（异于点C），利用三角形两边之和大于第三边可知DO+DA=DO+DB＞0B（半径），从而点D不在椭圆上.

      师：漂亮！因此有了圆心O和点A后，圆周上的每一点对应了一条折痕，每条折痕对应了轮廓线上的一个点，这些点所构成的图形即为椭圆.我们通过验证得出了以下结论.

      结论1：每条折痕上有且仅有一点在椭圆上，折痕即是切线.

      师：接下来大家相互讨论，图中若把线段AC看成入射光线，反射面是折痕，反射光线是什么？

      生众：反射光线是CO.

      师：如何验证呢？

      学生小组讨论.

      生6：如图4，由于∠1=∠2（中垂线性质），∠1=∠3（对顶角），则∠2=∠3，从而入射角等于反射角，即证明了椭圆的光学性质.

      

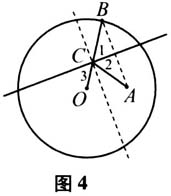      师：非常好，我们得到以下结论.

      结论2：椭圆的光学性质，即从椭圆的一个焦点发出的光线经过椭圆壁反射后，必经过椭圆的另一个焦点.

      设计意图 分析与解决问题，发挥学生学习主动性，师生合作分析问题，生生相互讨论问题，教师引领解决问题.教师要精心设计、创造问题情境，让学生通过自己动手实验研究、合作商讨，探索问题的结果.[3]

      ·环节3：理解与应用

      师：下面我们就来求椭圆的切线方程.

      例1 如图5，已知点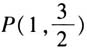在以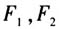为左、右焦点的椭圆C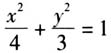：上，求椭圆C在点P处的切线l的方程.